2015-08-13
246
Знайти загальний розв’язок диференціального рівняння: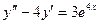 
.
Розв’язання
1. Запишемо однорідне рівняння, яке відповідає даному диференціальному рівнянню, та знайдемо його загальний розв’язок: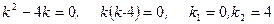 
,
.
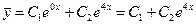2. 
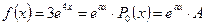, де А=3.
Один із коренів співпадає з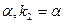 
, тому частинний розв’язок, згідно з таблицею (3.5), шукаємо у вигляді: 
.
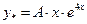Аналогічно з попередніми прикладами задача зводиться до визначення коефіцієнта А. Знаходимо першу, другу похідні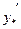 
, 
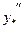та підставляємо в дане рівняння:
.
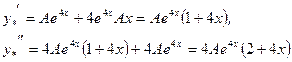
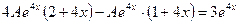
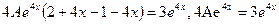Прирівнюючи коефіцієнти при однаковому множнику правої та лівої частин, знаходимо А: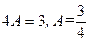 
,
частинний розв’язок: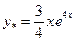 
.
3. Загальний розв’язок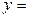 
.
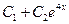
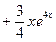5. Системи лінійних диференціальних рівнянь зі сталими коефіцієнтами
Система лінійних диференціальних рівнянь містить декілька невідомих функцій та їх похідні:
,
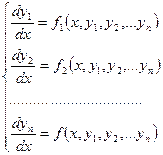де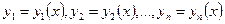 
- невідомі функції.
Метод розв’язання за допомогою виключення змінних зводить систему до одного диференціального рівняння від однієї невідомої функції порядку n, яке розв’язується одним з вище показаних способів. Інші невідомі функції визначають при підстановці знайденої функції в рівняння системи (як при розв’язанні систем алгебраїчних рівнянь). Ознайомимось з цим методом розв’язання на прикладі системи 2-х диференціальних рівнянь.
|
|
|
