Якщо функція є зростаючою (спадною) у кожній внутрішній точці проміжку (а;в), то вона називається зростаючою (спадною) на цьому проміжку.
Достатні ознаки: Якщо функція у=f(х) у внутрішній точці хо проміжку (а;в) має похідну f’(xo) i f’(xo)>0 (f’(xo)<0), то y=f(x) у точці хо зростає (спадає).
Завдання: Знайти проміжки, на яких функція
а) 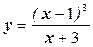 зростає; б)
зростає; б) 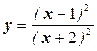 спадає.
спадає.
  №
п/п №
п/п
| План знаходження проміжків зростання та спадання функції | Застосування плану
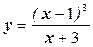 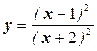
|
| 1. | Знаходимо область визначення ф-ії | Х+3 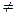 0
Д(у)= 0
Д(у)= 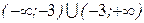
|
| 2. | Знаходимо похідну функції | 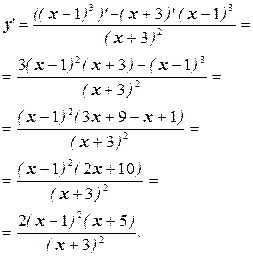
|
    3. 3.
| Функція зростає на проміжках, де y’>0; спадає на проміжках, де y’<0. | Y’>0
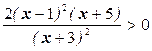 ; ; 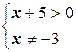 – +
о о
-5 -3 Х
– +
о о
-5 -3 Х
|
Відповідь: хЄ[-5;-3) 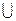 (-3;+
(-3;+ 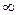 ).
).
Приклади: знайти проміжки, на яких функція
а) 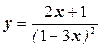 зростає; б)
зростає; б) 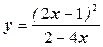 спадає.
спадає.
 2015-08-13
2015-08-13 492
492








