Вариант №1. 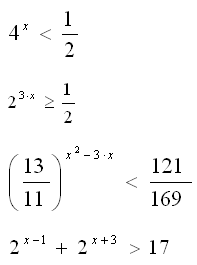
Вариант №2.
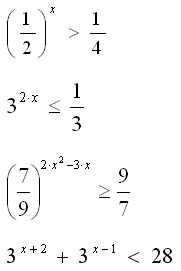
Оцените свою работу на уроке по 10 бальной шкале (поставьте свою точку на шкале).
Итоговый контроль. Самостоятельная работа по теме «Показательные уравнения и неравенства».
В – 1.
Каждому уравнению и неравенству сопоставьте решение:
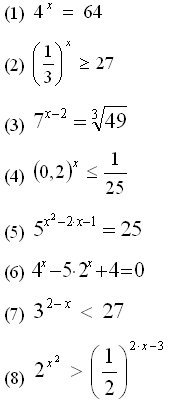
Решения:
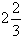 ,
,
-1,
x ≥–1,
x <3,
уравнение решений не имеет,
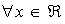 ,
,
x >2,
x ≤2,
неравенство решений не имеет,
0,
2,
x ≤–3,
3,
x >–1,
4,
x ≥–3,
x ≥2.
1) Продолжите: Показательным уравнением называется уравнение…,
2) Какое свойство показательной функции используется при решении неравенств? Сформулируйте его.
График функции 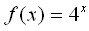 расположен ниже графика функции
расположен ниже графика функции 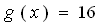 при
при 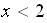 . Объясните почему.
. Объясните почему.
Решите неравенство (решение полностью обоснуйте)
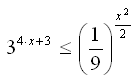
Докажите, что из неравенства x ≤3 следует неравенство 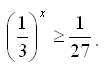 .
.
В – 2.
Каждому уравнению и неравенству сопоставьте решение:
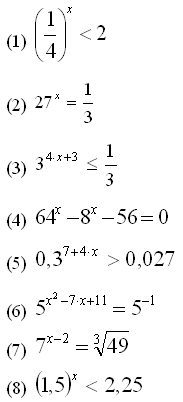
Решения:
5,
x ≤–2,
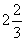 ,
,
x <–1,
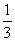 ,
,
x ≤–1,
3,
-1,
1,
–3≤ x ≤–1,
уравнение решений не имеет,
x >–1,
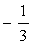 ,
,
неравенство решений не имеет,
2,
x <2,
0.
1) Продолжите: Показательным неравенством называется неравенство…
2) Какое свойство используется при решении показательных уравнений? Сформулируйте его.
|
|
|
График функции 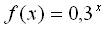 расположен ниже графика функции
расположен ниже графика функции 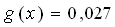 при x <3. Объясните почему.
при x <3. Объясните почему.
Решите неравенство (решение полностью обоснуйте)
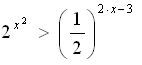
Докажите, что из неравенства x ≥5 следует неравенство 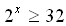 .
.
В этой статье я покажу как решать показательное неравенство вида 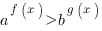
Решим неравенство:
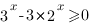
Запишем неравенство в таком виде:
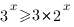
Разделим обе части неравенства на 3:
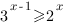
Теперь возьмем от обеих частей неравенства логарифм по основанию 3. Мы имеем право это сделать, так как обе части неравенства больше нуля. Основание логарифма больше единицы, поэтому знак неравенства не изменится.
Получим:
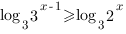
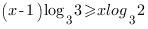
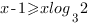
Перенесем слагаемые, содержащие неизвестное влево, а не содержащие – вправо:
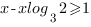
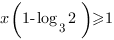
Разделим обе части неравенства на 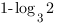 , предварительно исследовав знак этого выражения.
, предварительно исследовав знак этого выражения.
Т.к. 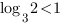
 ,
, 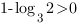
Получим:
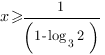
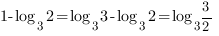
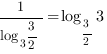 Ответ:
Ответ: 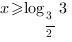
 В этой видеолекции показаны основные принципы решения всех типов показательных уравнений и неравенств. Я подробно рассказываю, как распознавать тип показательного уравнения и какие алгоритмы применять при решении уравнений и неравенств данного типа.
В этой видеолекции показаны основные принципы решения всех типов показательных уравнений и неравенств. Я подробно рассказываю, как распознавать тип показательного уравнения и какие алгоритмы применять при решении уравнений и неравенств данного типа.
Решение каждого задания представляет собой пошаговый разбор с подробными комментариями. Для самостоятельного освоения этой темы желательно сначала посмотреть видеолекцию, а потом попробовать решить эти же уравнения самостоятельно, используя презентацию. С помощью презентации вы можете продолжить решение задачи самостоятельно с любого шага решения.
В видеолекции подробно объяснено решение уравнений и неравенств:
1. Решить уравнение:
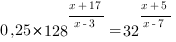
2. Решить неравенство:
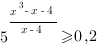
3. Решить уравнение:
|
|
|
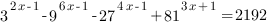
4. Решить неравенство:
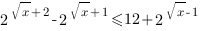

5. Решить уравнение:
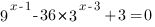
6. Решить неравенство:
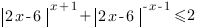
7. Решить уравнение:
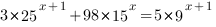
8. Решить неравенство:
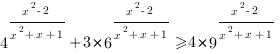
9. Решить уравнение:
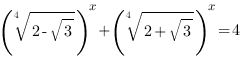
10. Решить неравенство:
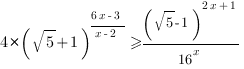
11. Решить неравенство:
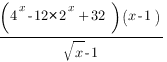

12. Решить неравенство:
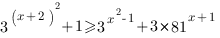
13. Решить неравенство:
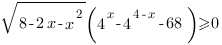
Показательные неравенства
· Неравенства вида ax>b (ax³b) или ax<b (ax£b), где a>0, a¹1, называются простейшими показательными неравенствами.
· Решение показательных неравенств основано на строгой монотонности показательной функции. Известно, что
o при основании, большем единицы, показательная функция возрастает,
o при положительном основании, меньшем единицы, показательная функция убывает.
· Неравенство вида
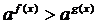
в зависимости от основания эквивалентно следующему:
o при a>1 f(x)>g(x);
o при 0<a<1 f(x)<g(x).
· Неравенство вида
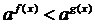
эквивалентно следующему неравенству:
o при a>1 f(x)<g(x);
o при 0<a<1 f(x)>g(x).
· Чтобы пользоваться свойством монотонности показательной функции следует путем надлежащих преобразований добиться одинаковых оснований в левой и правой частях неравенства.
Пример. Решить неравенство 16 x > 0,125.
Решение. Заметим, что 16=24, а 0,125=1/8=2-3. Тогда, переходя в обеих частях неравенства к основанию 2, получим 24 x > 2–3. Так как основание 2 > 1, то 4 х > –3, то есть x>-3/4.
Ответ: (-3/4;+¥).
Более сложные показательные неравенства сводятся к простейшим методами, аналогичными методам, используемым при решении показательных уравнений.
Пример 1. Решить неравенство 25х<6×5x-5.
Решение. Так как 25=52, то 25x=52x и данное неравенство примет вид:
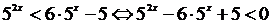 .
.
Заменой t=5x, t>0 сведем неравенство к квадратному:
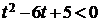 ,
,
решая которое методом интервалов, получим:
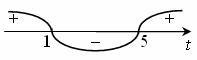
Следовательно, 1<t<5, то есть 1<5x<5, иначе 50<5x<51. Отсюда в силу свойства монотонности показательной функции получим, что 0<x<1.
Ответ: (0; 1).
Пример 2. Решить неравенство
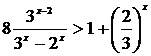 .
.
Решение. Числитель и знаменатель выражения в левой части данного неравенства разделим на 3х. В результате получим:
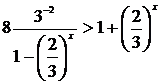 .
.
Сделав замену t=(2/3)x, t>0 будем иметь:
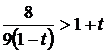
Решаем последнее неравенство:
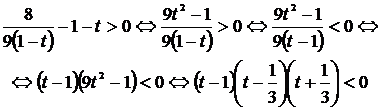 .
.
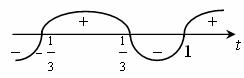
Пользуясь методом интервалов, получаем t<-1/3 или 1/3<t<1. Неравенство (2/3)x<-1/3 решений не имеет, а неравенство 1/3<(2/3)x<1 представим в виде
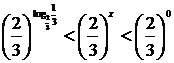
откуда 0<x<log2/3(1/3).
Ответ: (0; log2/3(1/3)).
·
Иногда показательные неравенства можно решить, используя свойства функций, входящих в обе части неравенства.
Пример. Решить неравенство 2x+3x+4x<3.
Решение. Каждая из функций y=2x, y=3x, y=4x непрерывна и возрастает на всей числовой оси. Значит такой же является и функция y=2x+3x+4x. Легко видеть, что при х=0 функция y=2x+3x+4x принимает значение 3. В силу непрерывности и монотонности этой функции при x>0 имеем 2x+3x+4x >3, при x<0 имеем 2x+3x+4x <3. Следовательно, решениями данного неравенства являются все x<0.
Ответ: (-¥; 0).
При решении показательных неравенств, приводящихся к квадратным неравенствам, поступают так же, как в примерах решения показательных уравнений, приводящихся к квадратным уравнениям, т. е. делают замену переменных, получают квадратное неравенство, которое решают, а затем возвращаются к прежней переменной.
Примеры.
Решить неравенство:
1) (0,5)2x+2<3∙(0,5)x.
Сделаем замену: пусть (0,5)х=у. Получаем неравенство:
у2+2<3y или y2-3y+2<0.
Разложим квадратный трехчлен y2-3y+2 на линейные множители по формуле:
ax2+bx+c=a (x-x1)(x-x2), где х1 и х2 – корни квадратного уравнения ax2+bx+c=0.
Находим корни приведенного квадратного уравнения y2- 3 y+ 2 =0. Дискриминант D=b2-4ac=32-4∙1∙2=9-8=1=12. Так как дискриминант является полным квадратом, то применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
у1+у2= 3, у1∙у2= 2. Отсюда: у1= 1, у2= 2. Значит, y2-3y+2=(у- 1)(у- 2).
Решаем неравенство: (у-1)(у-2)<0 методом интервалов.
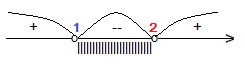
Получаем: ує(1; 2), отсюда: (0,5)хє(1; 2).
(0,5)х= 1 → (0,5)х= (0,5)0 → х=0.
(0,5)х= 2 → (1/2)x= 2 → 2— x= 21 → -x=1; x=-1. Значит, хє(-1; 0).
|
|
|
Ответ: (-1; 0).
2) 9x-1<3x-1+6.
Представим 9х-1 в виде степени числа 3.
32 (x-1)<3x-1+6. Сделаем замену: 3х-1=у. Тогда получается квадратное неравенство: у2<y+6. Переносим слагаемые в левую часть.
у2-у-6<0. Находим корни приведенного квадратного уравнения у2-у-6=0. Проверим, возможно ли применить теорему Виета, ведь ею пользуются только, если корни являются целыми числами. Гарантией этого будет дискриминант, который должен быть полным квадратом некоторого числа. Находим дискриминант D=b2-4ac=1-4∙(-6)=1+24=25=52. Дискриминант является полным квадратом числа 5, поэтому, подбираем корни, пользуясь теоремой Виета: у1+у2=1, у1∙у2=-6. Подходят значения: у1= -2 и у2= 3.
Раскладываем левую часть неравенства на линейные множители, получаем:
(у +2)(у- 3)<0. Решаем полученное неравенство методом интервалов.
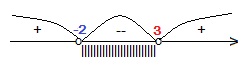
ує(-2; 3). Возвращаемся к переменной х:
3х-1є(-2; 3), но так как отрицательных значений степень 3х-1 принимать не может, то запишем: 3х-1є(0; 3). Определим интервал значений переменной х.
3х-1→ 0 при х-1 → -∞, так как число 3 в степени, стремящейся к минус бесконечности, фактически будет равным нулю, значит, х→ -∞.
Далее, 3х-1= 3 → 3х-1= 31 → х-1=1 → х=2.
Получили хє(-∞; 2).
Ответ: (-∞; 2).
Простейшими считаются показательные неравенства вида: ax<ay, ax>ay . (ax≤ay, ax≥ay).
Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют, если функция у=ах является возрастающей (а>1); eсли же показательная функция у=ах убывает (0<a<1), то знак нового неравенства меняют на противоположный:
ax < ay → x < y, если a>1; знак сохранен, так как функция возрастает;
ax < ay → x > y, если 0<a<1; функция убывает – знак поменялся;
ax > ay → x > y, если a>1; знак сохранен, так как функция возрастает
ax > ay → x < y, если 0<a<1; функция убывает – знак поменялся.
Примеры.
Решить неравенство:
1) 45-2x<0,25.
Представим правую часть в виде: 0,25=(25/100)=(1/4)=4-1;
45-2x<4-1; функция у=4х с основанием 4>1 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:
|
|
|
5-2x<-1;
— 2x<-1-5;
— 2x<-6 |:(-2) при делении обеих частей неравенства на отрицательное число, знак неравенства меняют на противоположный:
x>3.
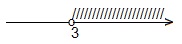
Ответ: (3; +∞).
2) 0,42х+1≥0,16.
Представим число 0,16 в виде степени числа 0,4. Получаем:
0,42х+1 ≥ 0,42; основание степеней – число 0,4 — удовлетворяет условию: 0<0,4<1; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:
2х+1 ≤ 2;
2х≤2-1;
2х≤1 |:2
x≤0,5.
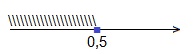
Ответ: (-∞; 0,5].
3) 23-x+21-x>40. Применим формулу: ax+y = ax∙ay. Запишем неравенство в виде:
23∙2-x+21∙2-x>40; Вынесем общий множитель за скобки:
2-x∙(23+21)>40; упрощаем левую часть:
2-x∙(8+2)>40;
2-x∙10>40 |:10
2-x>4;
2-x>22; основание степени — число 2>1, значит, знак неравенства сохраняем:
— x>2 |:(-1) при делении обеих частей неравенства на отрицательное число — знак неравенства меняют на противоположный:
x<-2.
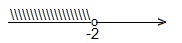
Ответ: (-∞; -2).
4) 3x+2+3x+1+3x≤39. Применяем формулу: ax∙ay=ax+y
3x∙32+3x∙31+3x≤39; вынесем общий множитель за скобки:
3x∙(32+31+1)≤39; упрощаем левую часть неравенства:
3x∙(9+3+1)≤39;
3x∙13≤39 |:13
3x≤3;
3x≤31; Показательная функция с основанием 3 (3>1) является возрастающей, поэтому, знак неравенства сохраним:
x≤1.
Ответ: (-∞; 1].
Простейшие показательные неравенства ax
Если основание а>1, то показательная функция возрастает, знак неравенства остается прежним.

Если основание 0<а<1, то показательная функция убывает, знак неравенства изменяется.
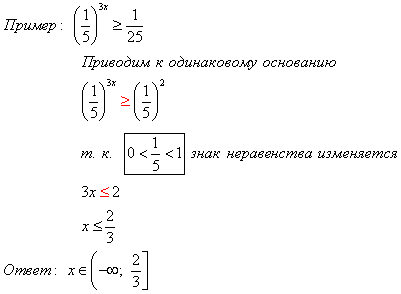
Методы решения показательных неравенств
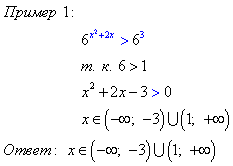
При решении показательных уравнений используют метод замены переменной.

 2015-08-13
2015-08-13 2816
2816







