Теория Учебный элемент № 1
Рассмотрим решение показательных неравенств вида 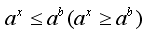 , где b – некоторое рациональное число. Если a >1, то показательная функция , где b – некоторое рациональное число. Если a >1, то показательная функция  монотонно возрастает и определена при всех х. Для возрастающей функции большему значению функции соответствует большее значение аргумента. Тогда неравенство монотонно возрастает и определена при всех х. Для возрастающей функции большему значению функции соответствует большее значение аргумента. Тогда неравенство 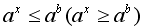 равносильно неравенству равносильно неравенству 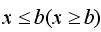 . Если 0< a <1, то показательная функция . Если 0< a <1, то показательная функция 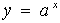 монотонно убывает и определена при всех х. Для убывающей функции большему значению функции соответствует меньшее значение аргумента. Тогда неравенство монотонно убывает и определена при всех х. Для убывающей функции большему значению функции соответствует меньшее значение аргумента. Тогда неравенство 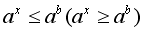 равносильно неравенству равносильно неравенству 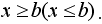
|
Рассмотрите приведенные ниже примеры решения показательных неравенств вида 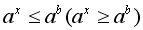 .
.
Пример 1. Решим неравенство 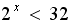
Запишем неравенство в виде 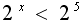 . Т. к.
. Т. к. 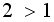 , то показательная функция
, то показательная функция 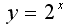 возрастает. Поэтому данное неравенство равносильно неравенству
возрастает. Поэтому данное неравенство равносильно неравенству 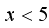 . Ответ:
. Ответ: 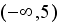 .
.
Пример 2. Решим неравенство 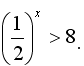 .
.
Запишем неравенство в виде 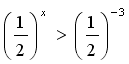 .
.
Т. к. 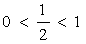 , то показательная функция
, то показательная функция 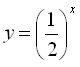 убывает. Поэтому данное неравенство равносильно неравенству
убывает. Поэтому данное неравенство равносильно неравенству 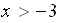 . Ответ:
. Ответ: 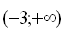 .
.
Решите неравенства:
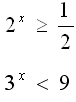
Дайте полное обоснование решения неравенств (см. примеры). Проконтролируйте правильность решения неравенств, сверив полученные ответы с ответами соседа по парте.
 2015-08-13
2015-08-13 474
474








