Прочитайте теорию (см. ниже). Занесите в тетрадь ту информацию, которую считаете нужной.
Теория
Рассмотрим решение показательных неравенств вида 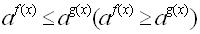 Где f (x) и g (x) некоторые функции зависящие от x. Частным случаем неравенств вида Где f (x) и g (x) некоторые функции зависящие от x. Частным случаем неравенств вида 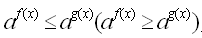 являются неравенства вида являются неравенства вида 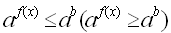 , где b – некоторое действительное число. Для решения неравенств рассмотренных видов используется свойство возрастания или убывания показательной функции. Решим неравенство , где b – некоторое действительное число. Для решения неравенств рассмотренных видов используется свойство возрастания или убывания показательной функции. Решим неравенство 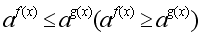 (*). Рассмотрим показательную функцию (*). Рассмотрим показательную функцию 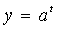 . И рассмотрим значения показательной функции . И рассмотрим значения показательной функции 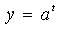 при t1=f(x) и при t2=g(x). Перепишем данное неравенство (*) в виде при t1=f(x) и при t2=g(x). Перепишем данное неравенство (*) в виде 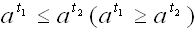 (**).
Если a >1, то функция (**).
Если a >1, то функция 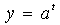 возрастает. Тогда неравенство (**) равносильно неравенству возрастает. Тогда неравенство (**) равносильно неравенству 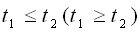 . А данное неравенство (*) неравенству . А данное неравенство (*) неравенству 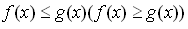 . Если 0< a <1, то функция . Если 0< a <1, то функция  убывает. Тогда неравенство (**) равносильно неравенству убывает. Тогда неравенство (**) равносильно неравенству 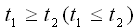 . А данное неравенство (*) неравенству . А данное неравенство (*) неравенству 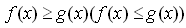 . .
|
Рассмотрите приведенные ниже примеры решения показательных неравенств вида 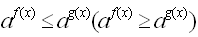
Пример 1. Решите неравенство 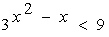
Запишем неравенство в виде 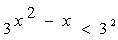 . Показательная функция
. Показательная функция 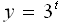 возрастает (3>1). Поэтому данное неравенство равносильно неравенству
возрастает (3>1). Поэтому данное неравенство равносильно неравенству 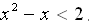 . Откуда
. Откуда 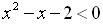 . Решив квадратное неравенство, получим –1< x <2. Ответ: (–1;2).
. Решив квадратное неравенство, получим –1< x <2. Ответ: (–1;2).
Пример 2. Решите неравенство 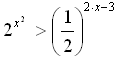
Запишем неравенство в виде 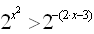 . Показательная функция
. Показательная функция 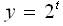 возрастает (2>1). Поэтому данное неравенство равносильно неравенству
возрастает (2>1). Поэтому данное неравенство равносильно неравенству 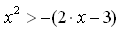 , откуда
, откуда 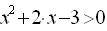 . Решив квадратное неравенство, получим x <–3 или x >1.
. Решив квадратное неравенство, получим x <–3 или x >1.
Ответ: 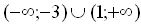 .
.
Решите неравенства. Дайте полное обоснование решения неравенств (см. примеры).
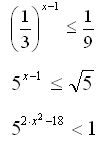
Проконтролируйте верность своего решения у соседа по парте.
 2015-08-13
2015-08-13 340
340








