2015-08-12
880
Не используя формул квадратное уравнение можно решить графическим способом. Например x 2 + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x 2; y = x + 1.
y = x 2, квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.
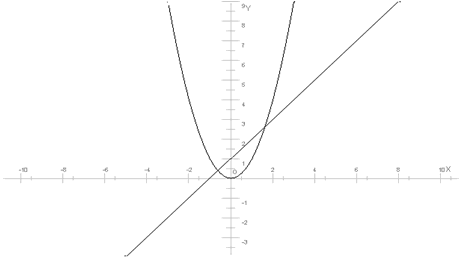
Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.
9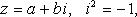 
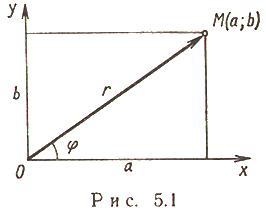
где i - мнимая единица; a - действительная часть: a = Re z; bi - мнимая часть: b = Im z; числа вида bi - чисто мнимые; плоскость Oxy - комплексная плоскость; ось Ох - действительная ось; ось Oy - мнимая ось;
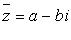- число, сопряженное числу z = a + bi;
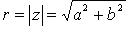- модуль комплексного числа;
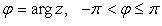либо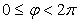 
, - аргумент комплексного числа z (главное значение аргумента);
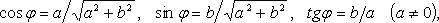
Arg z - множество аргументов числа z:
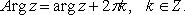
10 Действия над комплексными числами
Если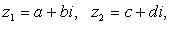 
то:
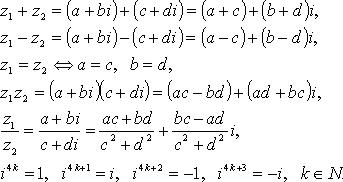
12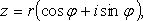 
где r - модуль;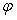 
- агрумент комплексного числа.
Если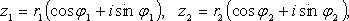 
то:
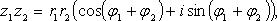
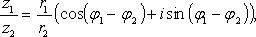
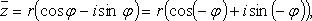
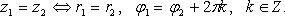
§ 26Пусть задана числовая функция с неограниченной сверху областью определения, то есть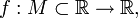 
и 
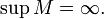Число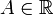 
называется пределом функции f при x стремящемся к бесконечности, если
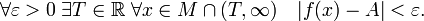
Пишут:
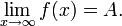
§ Аналогично пусть 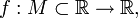и 
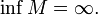Число 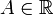называется пределом функции f при x стремящемся к минус бесконечности, если
|
|
|
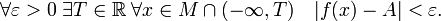
Пишут:
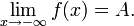
27Рассмотрим функцию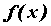 
, определенную на некотором промежутке 
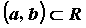. Функция 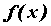непрерывна в точке 
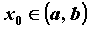, если предел функции в точке 
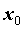равен значению функции в этой точке, 
.
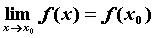ПРИМЕР 1. Доказательство непрерывности функции в точке.
Свойства функций, непрерывных на отрезке.
Функция, непрерывная в каждой точке промежутка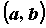 
, называется непрерывной на промежутке. Для функции, непрерывной на отрезке 
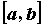, справедливы следующие утверждения.
Функция, непрерывная на отрезке 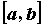, достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке 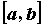существуют точки 
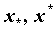такие, что
.
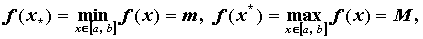
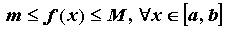Если функция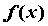 
непрерывна на отрезке 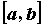и принимает на концах значения разных знаков, то на интервале 
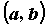существует точка 
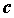, в которой функция обращается в нуль, т.е. 
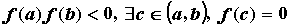. Это утверждение применяют для отделения корней уравнений 
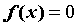с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.
Если функция 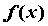непрерывна на отрезке 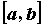, дифференцируема хотя бы на интервале 
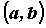, то на интервале 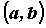существует точка 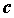, такая, что 
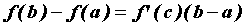. Это свойство называют формулой Лагранжа или формулой конечных приращений.
56 Арккотангенсом числа m называется такое значение угла x, для которого 
Функция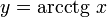 
непрерывна и ограничена на всей своей числовой прямой. Функция 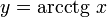является строго убывающей.
§ 
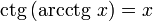при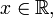 
§ 
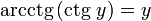при 0 < y < π,
§ 
§ 
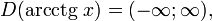
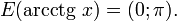
[править] Свойства функции arcctg
§ 
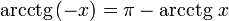(график функции центрально-симметричен относительно точки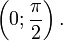 
|
|
|
§ 
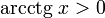при любых x.
§ 
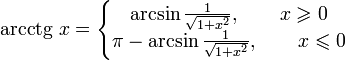
[править] Получение функции arcctg
Дана функция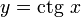 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие 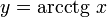функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз — (0;π). На этом отрезке 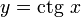строго убывает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция 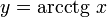, график которой симметричен графику 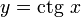на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу
32 Логарифмирование, действие, заключающееся в нахождении логарифма числового, алгебраического или иного выражения. Логарифмирование - одно из двух действий, обратных возведению в степень: если ab = с, то a =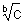 
и b = logac
34 Простейшим показательным уравнением
Простейшим показательным уравнением является уравнение ах=b, где а и b - некоторые положительные числа (а?1), х - неизвестная величина.1) при b?0 не имеет корней; 2) при b>0 имеет единственный корень x=logab.
Пример1. 2х=64
Решение: 2х=26 - основания равны, степени равны, значит равны и показатели. х=6
Ответ х=6
Пример 2. 25х=-25
Решение: т.к. -25<0, то уравнение не имеет корней
Ответ: нет корней.
Пример 3. Решить уравнение 8cos x =5.
Решение: cos x = log85 поскольку -185<1, то x=±arccos log85+2?n, n?.
Ответ: x=±arccos log85+2?n, n?.
