Содержание
| §1. | КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ | |
| §2 | ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ | |
| §3. | ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ | |
| §4 | ПРЕДЕЛ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. НЕПРЕРЫВНОСТЬ | |
| §5. | ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ УСЛОВИЯ КОШИ-РИМАНА | |
| §6 | ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ | |
| §7. | ИНТЕГРАЛЬНАЯ ТЕОРЕМА КОШИ. ФОРМУЛА КОШИ | |
| §8. | РАВНОМЕРНАЯ СХОДИМОСТЬ ФУНКЦИОНАЛЬНОГО РЯДА ТЕОРЕМА АБЕЛЯ | |
| §9. | РЯД ТЕЙЛОРА НУЛИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ | |
| §10. | РЯД ЛОРАНА ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ | |
| §11. | ВЫЧЕТЫ ОСНОВНАЯ ТЕОРЕМА О ВЫЧЕТАХ. | |
| §12. | ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ С ПОМОЩЬЮ ВЫЧЕТОВ | |
| ЛИТЕРАТУРА |
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Уже простейшие алгебраические операции над действительными числами (извлечение квадратного корня из отрицательного числа, решение квадратного уравнения с отрицательным дискриминантом) выводят за пределы множества действительных чисел. Дальнейшее обобщение понятия числа приводит к комплексным числам. Замечательным свойством множества комплексных чисел является его замкнутость относительно основных математических операций. Иначе говоря, основные математические операции над комплексными числами не выводят из множества комплексных чисел.
Комплексным числом 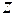 (в алгебраической форме) называется выражение
(в алгебраической форме) называется выражение
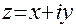
где 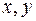 – произвольные действительные числа,
– произвольные действительные числа, 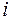 – мнимая единица, определяемая условием
– мнимая единица, определяемая условием 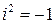 .
.
Число 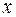 называется действительной частью комплексного числа
называется действительной частью комплексного числа 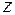 , обозначается
, обозначается 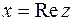 (от латинского «realis»), число
(от латинского «realis»), число 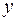 называется мнимой частью комплексного числа
называется мнимой частью комплексного числа 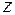 и обозначается
и обозначается 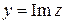 (от латинского «imaginarius»).
(от латинского «imaginarius»).
Два комплексных числа 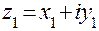 и
и 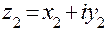 равны тогда и только тогда, когда равны их действительные и мнимые части:
равны тогда и только тогда, когда равны их действительные и мнимые части: 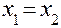 ,
, 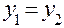 . Два комплексных числа равны либо не равны (понятия «больше» и «меньше» для комплексных чисел не вводятся).
. Два комплексных числа равны либо не равны (понятия «больше» и «меньше» для комплексных чисел не вводятся).
Комплексно-сопряженным к числу 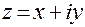 называется число
называется число 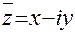 . Очевидно, комплексно–сопряженное число к числу
. Очевидно, комплексно–сопряженное число к числу 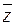 совпадает с числом
совпадает с числом 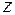 :
: 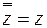 .
.
Арифметические операции. Сложение, вычитание и умножение комплексных чисел производят по обычным правилам алгебры.
Пусть 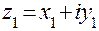 ,
, 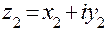 . Тогда
. Тогда
сумма 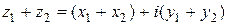 ,
,
разность 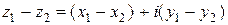 ,
,
произведение 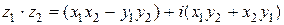 ,
,
частное (при 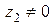 )
)

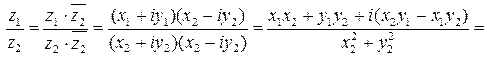
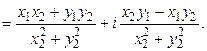

Пример 1. Заданы комплексные числа 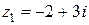 ,
, 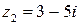 .
.
Найти 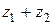 ,
, 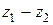 ,
, 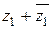 .
.
Решение. 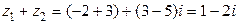 ;
;
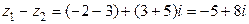 ;
;
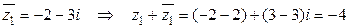 .
.
Задача 1. Пусть 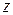 и
и 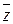 – пара комплексно-сопряженных чисел. Показать, что их сумма есть действительное число, разность – мнимое число, а произведение есть действительное неотрицательное число.
– пара комплексно-сопряженных чисел. Показать, что их сумма есть действительное число, разность – мнимое число, а произведение есть действительное неотрицательное число.
Пример 2. Найти 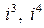 ,
, 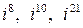 .
.
Решение. 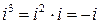 ;
; 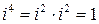 .
.
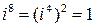 ,
, 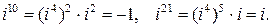
Замечание. Степени числа 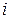 можно представить в виде таблицы
можно представить в виде таблицы
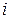 | 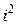 | 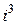 | 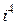 | 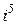 | 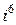 | 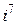 | 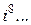 |
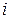 | 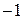 | 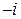 | 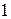 | 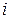 | 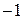 | 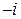 | 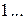 |
Пример 3. Перемножить числа 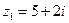 и
и 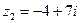 .
.
Решение. 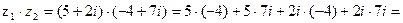
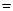
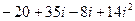
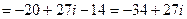
Пример 4. Вычислить а) 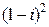 ; б)
; б) 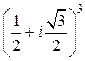 ; в)
; в) 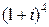 .
.
Решение.
а) Раскроем квадрат разности:
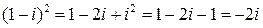 .
.
б) Раскроем куб суммы:
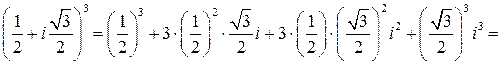
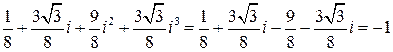 .
.
в) По биному Ньютона:
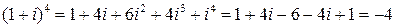 .
.
Можно было считать так: 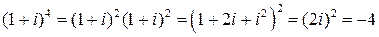 .
.
Пример 5. Найти частное 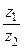 , если
, если 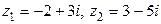 .
.
Решение.
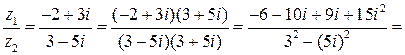
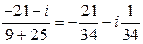 .
.
Пример 6. Вычислить а) 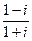 , б)
, б)  .
.
Решение. а) 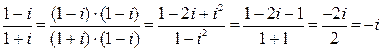 .
.
б) 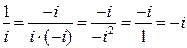 .
.
Запомним: 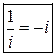
Геометрическая интерпретация комплексного числа. 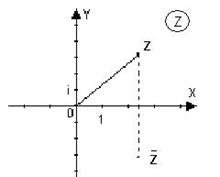
Рассмотрим декартову прямоугольную систему координат. Отложим по оси абсцисс действительную часть 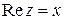 комплексного числа
комплексного числа 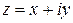 , а по оси ординат – его мнимую часть
, а по оси ординат – его мнимую часть 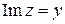 . Получим точку с координатами
. Получим точку с координатами 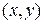 . При этом каждому комплексному числу
. При этом каждому комплексному числу 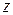 соответствует одна точка плоскости. Верно и обратное: каждой точке
соответствует одна точка плоскости. Верно и обратное: каждой точке 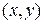 плоскости можно поставить в соответствие комплексное число
плоскости можно поставить в соответствие комплексное число 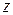 , действительная часть которого
, действительная часть которого 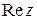 равна абсциссе точки, а мнимая часть
равна абсциссе точки, а мнимая часть 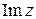 равна ординате точки. Таким образом, между комплексными числами и точками плоскости устанавливается взаимно однозначное соответствие. (Ранее мы говорили о взаимно однозначном соответствии между действительными числами и точками числовой прямой).
равна ординате точки. Таким образом, между комплексными числами и точками плоскости устанавливается взаимно однозначное соответствие. (Ранее мы говорили о взаимно однозначном соответствии между действительными числами и точками числовой прямой).
Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью. Для отличия её от действительной плоскости в правом верхнем углу пишут букву 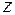 , обведенную кружком. Ось абсцисс на такой плоскости называют действительной осью, а ось ординат – мнимой осью. Комплексно-сопряженное число – это зеркальное отражение заданного комплексного числа относительно действительной оси. Начало координат называется нуль-точкой. Расстояние комплексного числа от начала координат называется модулем этого числа:
, обведенную кружком. Ось абсцисс на такой плоскости называют действительной осью, а ось ординат – мнимой осью. Комплексно-сопряженное число – это зеркальное отражение заданного комплексного числа относительно действительной оси. Начало координат называется нуль-точкой. Расстояние комплексного числа от начала координат называется модулем этого числа:
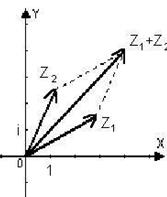
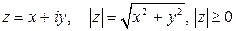 .
.
Задача 2. Доказать, что 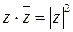 .
.
Модуль разности двух комплексных чисел – это расстояние между соответствующими точками:
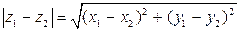 .
.
Каждой точке комплексной плоскости поставим в соответствие вектор с началом в нуль-точке и концом в данной точке. Очевидно, это соответствие взаимно однозначно. В такой интерпретации действительная и мнимая части комплексного числа – это первая и вторая компоненты вектора. Сумма 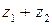 представляется теперь диагональю параллелограмма, построенного на векторах
представляется теперь диагональю параллелограмма, построенного на векторах 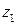 и
и 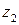 , разность
, разность 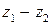 понимается как
понимается как 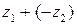 . Модуль комплексного числа представляет собой длину вектора. Геометрически очевидным является неравенство треугольника в комплексной плоскости:
. Модуль комплексного числа представляет собой длину вектора. Геометрически очевидным является неравенство треугольника в комплексной плоскости: 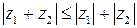 .
.
Пример 7. Указать геометрическое место точек на комплексной плоскости, для которых
а) 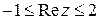 ; ; | б) 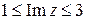 ; ; |
в) 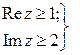 ; ; | г) 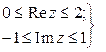 . . |
Решение. а) Так как 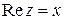 , то заданное двойное неравенство можно переписать в виде:
, то заданное двойное неравенство можно переписать в виде: 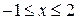 . Получили вертикальную полосу.
. Получили вертикальную полосу.
б) Так как 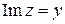 , то заданное двойное неравенство перепишем в виде:
, то заданное двойное неравенство перепишем в виде: 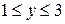 . Получили горизонтальную полосу. Задачи в) и г) решить самостоятельно.
. Получили горизонтальную полосу. Задачи в) и г) решить самостоятельно.
Пример 8. Указать геометрическое место точек на комплексной плоскости, для которых а) 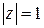 ; б)
; б) 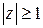 ; в)
; в) 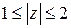 .
.
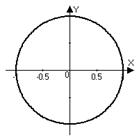
Решение. а) Модуль комплексного числа 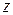 – это длина вектора, идущего из нуль-точки в точку
– это длина вектора, идущего из нуль-точки в точку 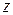 , т.е. расстояние от начала координат до точки
, т.е. расстояние от начала координат до точки 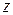 . Значит, в случае
. Значит, в случае 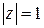 речь идет о геометрическом месте точек плоскости, равноудаленных от начала координат – это окружность (в данном случае радиус окружности равен 1). Можно было перевести задачу на язык декартовых координат:
речь идет о геометрическом месте точек плоскости, равноудаленных от начала координат – это окружность (в данном случае радиус окружности равен 1). Можно было перевести задачу на язык декартовых координат:
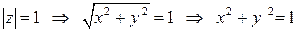 .
.
б) Здесь речь идет о геометрическом месте точек, находящихся вне круга радиуса 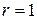 (с центром в начале координат).
(с центром в начале координат).
в) точки находятся в кольце между окружностями радиуса 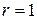 и
и 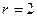 .
.
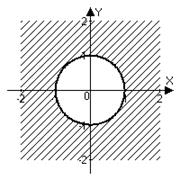
Пример 9. Указать геометрическое место точек на комплексной плоскости, для которых а) 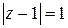 ; б)
; б) 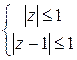 ; в)
; в) 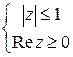 .
.
Решение. а) Модуль разности 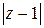 – это расстояние между точкой
– это расстояние между точкой 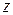 комплексной плоскости и точкой 1. Значит, речь идет о геометрическом месте точек, равноудаленных (на расстояние 1) от точки 1, – это окружность радиуса 1 с центром в точке (1;0). На языке координат:
комплексной плоскости и точкой 1. Значит, речь идет о геометрическом месте точек, равноудаленных (на расстояние 1) от точки 1, – это окружность радиуса 1 с центром в точке (1;0). На языке координат:
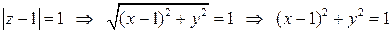 .
.
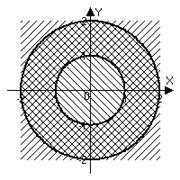
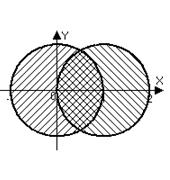
б) Точки находятся одновременно в круге 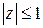 с центром в начале координат и в круге
с центром в начале координат и в круге 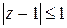 с центром, смещенным в точку
с центром, смещенным в точку 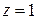 :
: 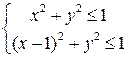 .
.
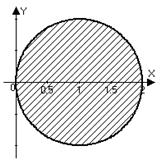
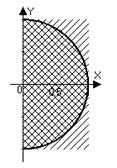
в) Это точки правой полуплоскости 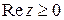 , лежащие внутри круга
, лежащие внутри круга 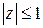 :
: 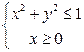 .
.
: 
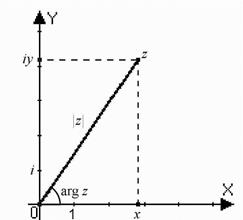
Тригонометрическая форма комплексного числа. Аргументом комплексного числа 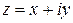 называют угол
называют угол 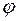 , который составляет вектор
, который составляет вектор 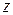 с положительным направлением действительной оси,
с положительным направлением действительной оси, 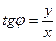 . Этот угол определяется неоднозначно:
. Этот угол определяется неоднозначно:
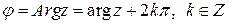 .
.
Здесь 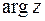 – главное значение аргумента, оно выделяется неравенствами
– главное значение аргумента, оно выделяется неравенствами 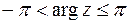 (т.е. на комплексной плоскости проводится разрез по действительной оси влево от начала координат).
(т.е. на комплексной плоскости проводится разрез по действительной оси влево от начала координат).
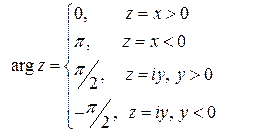 | 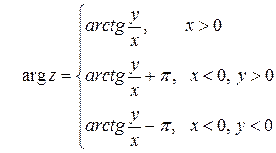 |
В первом столбце 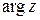 указан для числа
указан для числа 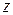 , лежащего на действительной или мнимой оси, а во втором столбце - для всех остальных комплексных чисел.
, лежащего на действительной или мнимой оси, а во втором столбце - для всех остальных комплексных чисел.
Обозначим 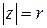 . Так как
. Так как 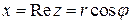 ,
, 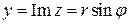 , то комплексное число можно представить в тригонометрической форме:
, то комплексное число можно представить в тригонометрической форме:
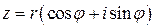 .
.
Два комплексных числа 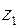 и
и 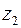 , заданных в тригонометрической форме
, заданных в тригонометрической форме
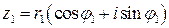 ,
, 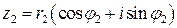 ,
,
в силу неоднозначности аргумента равны тогда и только тогда, когда 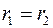 ,
, 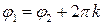 .
.
Пример 10. Найти модули и аргументы, а также главные значения аргументов комплексных чисел 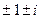 . Записать каждое из них в тригонометрической форме.
. Записать каждое из них в тригонометрической форме.
Решение. Модули всех этих чисел одинаковы:
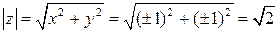 .
.
Аргумент каждого числа находим, учитывая четверть, в которой лежит соответствующая точка.
1) Точка 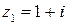 лежит в первой четверти, значит,
лежит в первой четверти, значит,
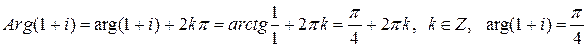 .
.
В тригонометрической форме 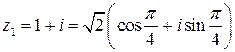 , здесь учтена
, здесь учтена 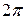 - периодичность косинуса и синуса.
- периодичность косинуса и синуса.
2) Точка 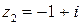 лежит во второй четверти, значит,
лежит во второй четверти, значит,
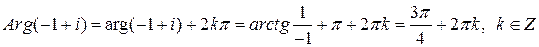 ,
,
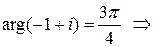
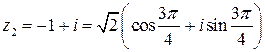 .
.
3) Точка 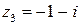 лежит в третьей четверти, значит,
лежит в третьей четверти, значит,
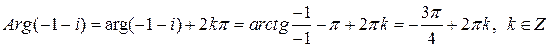 ,
,
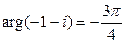 .
.
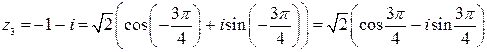 .
.
4) Точка 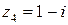 лежит в четвертой четверти, значит,
лежит в четвертой четверти, значит,
 ,
,
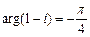 .
.
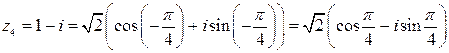 .
.
Умножение и деление комплексных чисел в тригонометрической форме. Пусть числа 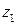 и
и 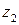 заданы в тригонометрической форме:
заданы в тригонометрической форме: 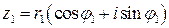 ,
, 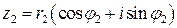 . Перемножим их:
. Перемножим их:
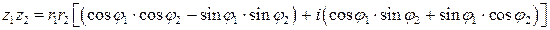 .
.
Вспоминая формулы для косинуса и синуса суммы двух углов, получаем
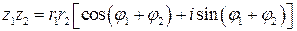 . (1)
. (1)
Мы видим, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Геометрический смысл этой операции: представляя числа 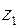 и
и 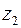 векторами на комплексной плоскости, исходящими из нуль-точки, видим, что вектор
векторами на комплексной плоскости, исходящими из нуль-точки, видим, что вектор 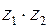 получается из вектора
получается из вектора 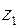 «растяжением» в
«растяжением» в 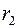 раз и поворотом на угол
раз и поворотом на угол 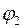 .
.
Для частного получаем формулу:
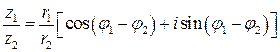 . (2)
. (2)
Пример 11. Найти произведение и частное чисел
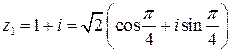 и
и 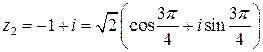 .
.
Решение. В соответствии с формулой (1) запишем:
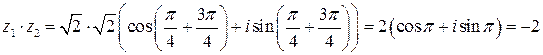 .
.
Проверим результат, перемножая эти числа в алгебраической форме:
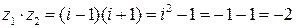 .
.
По формуле (2) находим
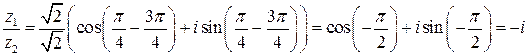 .
.
В алгебраической форме эта операция запишется так:
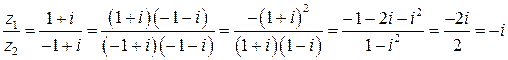 .
.
Возведение комплексного числа в степень. Из формулы (1) следует, что возведение в степень 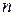 комплексного числа
комплексного числа 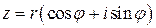 производится по правилу
производится по правилу
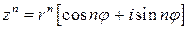 . (3)
. (3)
Пример 12. Вычислить 1) 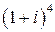 ; 2)
; 2) 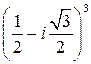 .
.
Решение. 1) Выше мы получили запись комплексного числа 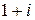 в тригонометрической форме:
в тригонометрической форме: 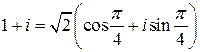 . По формуле (3) находим
. По формуле (3) находим 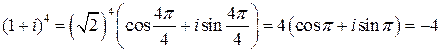 . Этот же результат был получен выше в примере 4в) с помощью бинома Ньютона.
. Этот же результат был получен выше в примере 4в) с помощью бинома Ньютона.
2) Прежде всего представим число 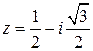 в тригонометрической форме.
в тригонометрической форме.
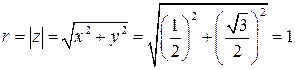 ,
, 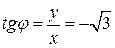 ,
,
точка 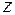 лежит в четвертой четверти, значит,
лежит в четвертой четверти, значит, 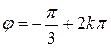 . Поэтому
. Поэтому
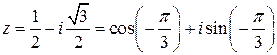 .
.
Остается воспользоваться формулой (3):
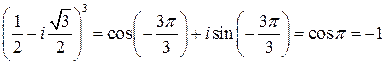 .
.
Раскрывая куб разности, получим тот же результат (проверьте!).
При 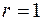 формула (3) превращается в формулу Муавра:
формула (3) превращается в формулу Муавра:
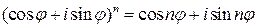 . (4)
. (4)
С её помощью легко получаются соотношения, выражающие синусы и косинусы кратных углов с 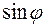 и
и 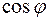 .
.
Пример 13. Выразить 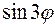 и
и 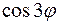 через
через 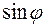 и
и 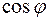 .
.
Решение. Полагая в формуле Муавра 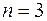 , получим:
, получим:
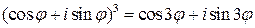 .
.
Слева раскроем куб суммы и соберем подобные члены:
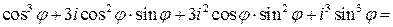
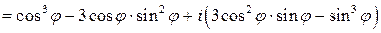 .
.
Здесь учтено, что 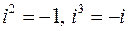 . Пришли к равенству двух комплексных чисел в алгебраической форме
. Пришли к равенству двух комплексных чисел в алгебраической форме
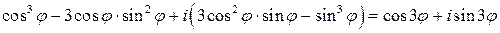 ,
,
которое справедливо в том и только в том случае, когда равны действительные и мнимые части этих чисел.
Равенство действительных частей дает 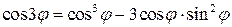 ;
;
приравнивая мнимые части, получаем 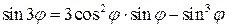 .
.
Извлечение корня из комплексного числа. Если комплексные числа 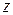 и
и 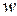 связаны соотношением
связаны соотношением 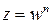 , то
, то 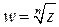 . Представим числа
. Представим числа 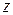 и
и 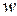 в тригонометрической форме:
в тригонометрической форме:
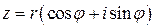 ,
, 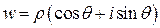 .
.
Будем считать, что здесь 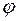 – главное значение аргумента числа
– главное значение аргумента числа 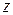 .
.
Наша задача – по заданному числу 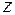 (т.е. по известным
(т.е. по известным 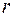 и
и 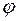 ) определить
) определить 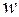 (т.е.
(т.е. 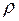 и
и 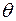 ). В соответствии с формулой (3) равенство
). В соответствии с формулой (3) равенство 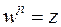 запишется в виде
запишется в виде
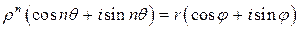 .
.
Из равенства двух комплексных чисел в тригонометрической форме следует:
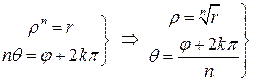 .
.
Здесь 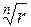 – корень
– корень 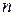 -ой степени из действительного неотрицательного числа. Значит, для корня
-ой степени из действительного неотрицательного числа. Значит, для корня 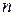 -ой степени из комплексного числа
-ой степени из комплексного числа 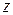 получаем формулу
получаем формулу
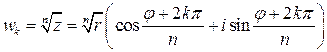 . (5)
. (5)
Полагая последовательно 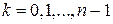 , получим
, получим 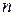 различных значений
различных значений 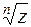 :
:
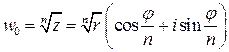 ,
,
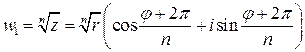 ,
,
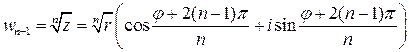 .
.
Все эти корни имеют одинаковые модули 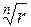 , т.е. соответствующие точки располагаются на окружности радиуса
, т.е. соответствующие точки располагаются на окружности радиуса 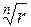 с центром в начале координат. Аргументы двух соседних корней отличаются на угол
с центром в начале координат. Аргументы двух соседних корней отличаются на угол 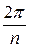 . Значит, все значения корня
. Значит, все значения корня 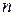 -ой степени из комплексного числа
-ой степени из комплексного числа 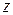 находятся в вершинах правильного
находятся в вершинах правильного 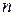 -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса 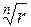 .
.
Пример 14. Найти все значения корня 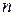 -ой степени из комплексного числа
-ой степени из комплексного числа 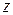 и изобразить их на комплексной плоскости, если
и изобразить их на комплексной плоскости, если
1) 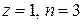 , 2)
, 2) 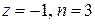 , 3)
, 3) 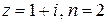 , 4)
, 4) 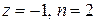 .
.
Решение. 1) Прежде всего, найдем модуль и аргумент комплексного числа 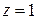 :
: 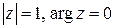 . Формула (5) для
. Формула (5) для 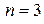 примет вид
примет вид
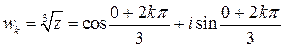 ,
,
откуда 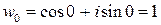 ,
,
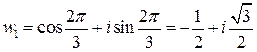 ,
,
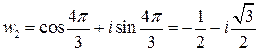 .
.
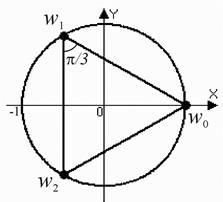
Точки 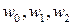 находятся в вершинах правильного треугольника, вписанного в окружность единичного радиуса, один корень –
находятся в вершинах правильного треугольника, вписанного в окружность единичного радиуса, один корень – 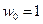 является действительным числом. Аргументы двух соседних точек отличаются на угол
является действительным числом. Аргументы двух соседних точек отличаются на угол 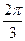 . Заметим, что
. Заметим, что 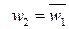 .
.
2) Здесь 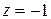 :
: 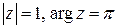 , поэтому
, поэтому
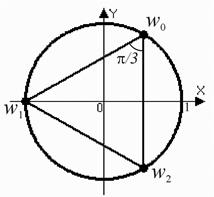
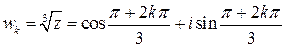 ,
,
откуда 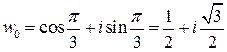 ,
,
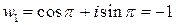 ,
,
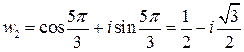 .
.
Точки 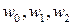 находятся в вершинах правильного треугольника, вписанного в окружность
находятся в вершинах правильного треугольника, вписанного в окружность 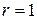 , корень
, корень 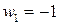 является действительным числом. Заметим, что
является действительным числом. Заметим, что 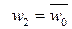 . Сравните с результатом пр.12.2, где получили
. Сравните с результатом пр.12.2, где получили 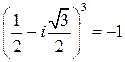 , т.е.
, т.е. 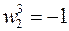 .
.
3) Здесь 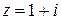 :
: 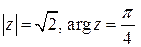 и при
и при 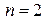
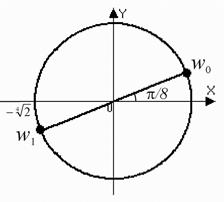
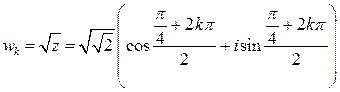 ,
,
откуда 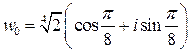 ,
,
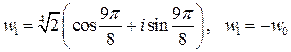 .
.
4) Здесь 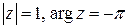 и при
и при 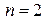
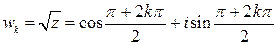 , откуда получаем два числа:
, откуда получаем два числа:
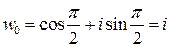 ,
, 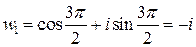 .
.
Запомним: 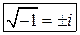 .
.
Задача 3. Выполнить задания пр.14, если 1) 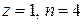 , 2)
, 2) 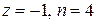 .
.
Пример 15. Разложить на линейные множители квадратный трехчлен
1) 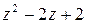 ; 2)
; 2) 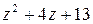 .
.
Решение. 1) Рассмотрим квадратное уравнение 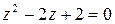 . Его дискриминант
. Его дискриминант 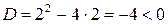 . Значит, действительных корней нет. Из пр.14.4 следует, что
. Значит, действительных корней нет. Из пр.14.4 следует, что 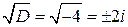 . По формуле для корней квадратного уравнения
. По формуле для корней квадратного уравнения 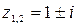 . Получили два комплексно-сопряженных корня
. Получили два комплексно-сопряженных корня 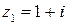 и
и 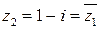 . В соответствии с найденными корнями можем разложить квадратный трехчлен на линейные множители:
. В соответствии с найденными корнями можем разложить квадратный трехчлен на линейные множители:
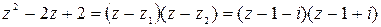 .
.
2) Рассмотрим квадратное уравнение 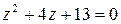 . Его дискриминант
. Его дискриминант 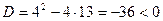 , действительных корней нет. Из пр.14.4 следует, что
, действительных корней нет. Из пр.14.4 следует, что 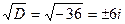 . По формуле для корней квадратного уравнения
. По формуле для корней квадратного уравнения 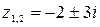 . Получили два комплексно-сопряженных корня
. Получили два комплексно-сопряженных корня 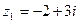 и
и 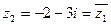 . В соответствии с найденными корнями разлагаем квадратный трехчлен на линейные множители:
. В соответствии с найденными корнями разлагаем квадратный трехчлен на линейные множители:
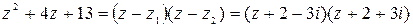 .
.
Обращаем внимание на то, что квадратное уравнение с действительными коэффициентами имеет пару комплексно сопряженных корней.
Задача 4. Убедиться, что справедливы разложения на линейные множители
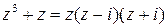 ;
; 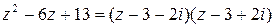 ;
; 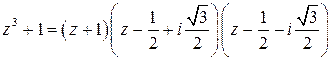 .
.
Показательная форма комплексного числа. Формула Эйлера (будет доказана позже):
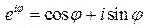 , (6)
, (6)
позволяет записать комплексное число в показательной форме:
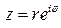 , где
, где 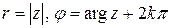 .
.
Из формулы Эйлера и из 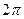 - периодичности синуса и косинуса следует:
- периодичности синуса и косинуса следует:
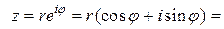
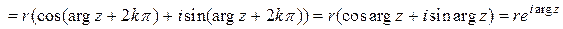 .
.
Значит, 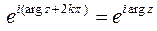 , т.е.
, т.е. 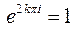 .
.
Пример 16. Числа 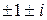 записать в показательной форме.
записать в показательной форме.
Решение. В примере 10 нашли 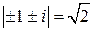 ,
,
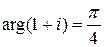 ,
, 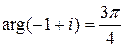 ,
, 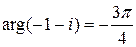 ,
, 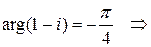
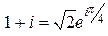 ,
, 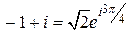 ,
, 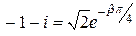 ,
, 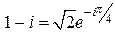 .?
.?
Легко проверить справедливость соотношений:
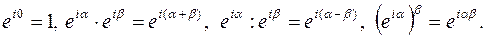
Сравните эти соотношения с правилами умножения, деления и возведения в степень комплексных чисел в тригонометрической форме.
Пример 17. Сравните комплексные числа 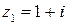 и
и 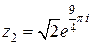 .
.
Решение. Из пр.16: 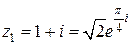 . У чисел
. У чисел 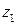 и
и 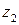 модули равны. Выделяя в показателе числа
модули равны. Выделяя в показателе числа 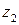 слагаемое, кратное
слагаемое, кратное 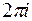 , представим
, представим 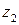 в виде
в виде 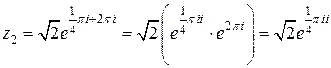 , так как множитель
, так как множитель 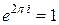 . Значит,
. Значит, 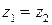 .
.
 2015-05-13
2015-05-13 130795
130795