Корни многочлена

Расмотрим многочлен:

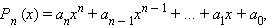, где a1, a2,..., an − целые числа, an ≠ 0.

Если многочлен 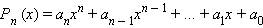с целыми коэффициентами имеет рациональный корень 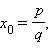, то число p является делителем числа 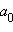(свободного члена), а число q является делителем числа 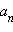(старшего коэффициента).

Доказательство:

Действительно, если число 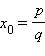является корнем многочлена 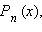, то 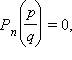. А именно: 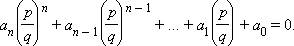. Умножим обе части этого уравнения

на 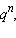, получим: 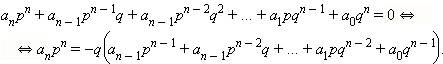. Так как

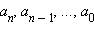- целые числа, то в скобке стоит целое число. Значит, вся правая часть этого равенства делится на q, так как q входит в неё в качестве сомножителя. А значит и левая часть тождества делится на q, так как она равна правой. Число p не делится на q, так как иначе дробь 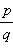была бы сократимой, значит и 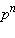не делится на q. Следовательно, на q делится единственный из оставшихся сомножителей левой части, а именно 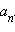. Теорема доказана!