Вертикальных электродов

Рассмотрим систему из N₁ вертикальных анодных и ка­тодных электродов (рис. 4.31), параметры системы в вертикальной плоскости аналогичны приведённым на рис. 4.30.

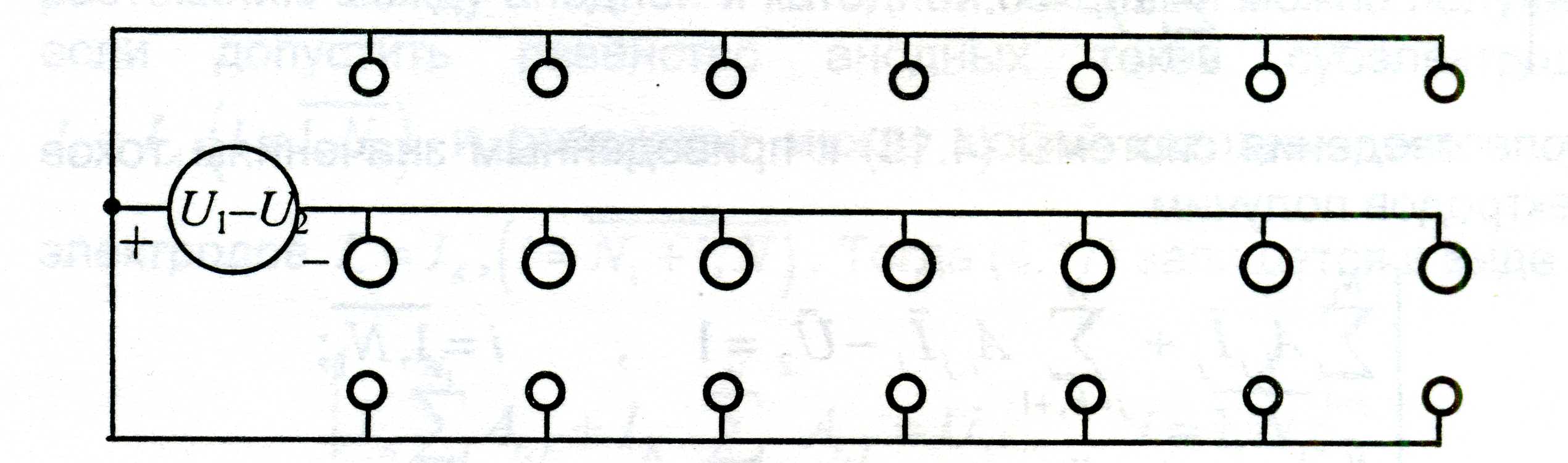
Рис.4.31. Система анодных и катодных секций

Вводя сквозную нумерацию электродов (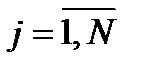) — аноды, 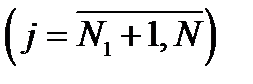— катоды (где N = N₁+N₂), связь между потенциалами и токами в такой системе запишем через потенциальные коэффициенты в виде [12], [13], [14]

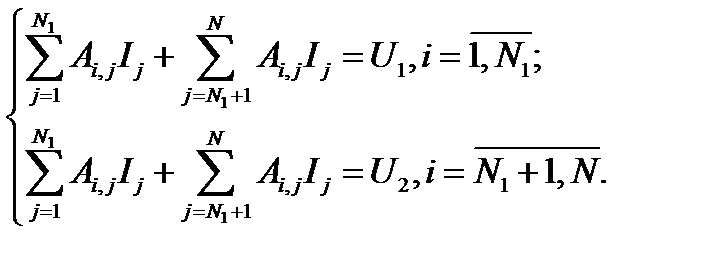(4.17)

Перейти к приведённым значениям тока 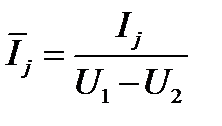в системе (4.17) можно несколькими способами.

Способ 1. Прибавим и отнимем U₂ в правых частях уравне­ний системы (4.17) для 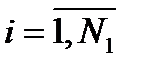. Перенесём потенциал U₂ во всех уравнениях полученной системы в левую часть. При этом количество неизвестных в этой системе станет N+1, поэтому, до­бавляя к полученным уравнениям дополнительное условие элек­тронейтральности системы электродов, получим СЛАУ размером (N + 1) x (N + 1):

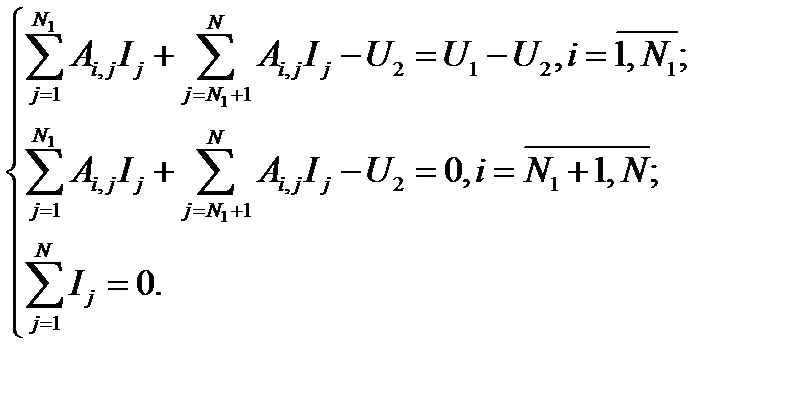(4.18)

После сведения системы (4.18) к приведенным значениям токов электродов получим

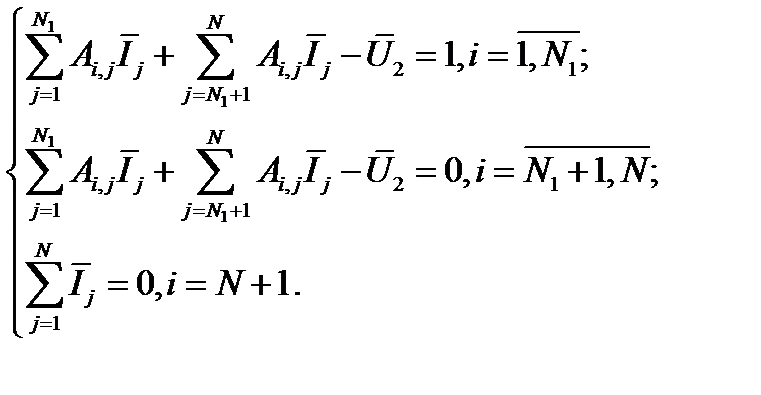
После нахождения из последней системы значений 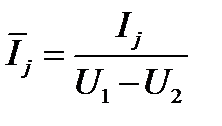сопротивление растекания между анодной и катодной секциями электродов можно определить как

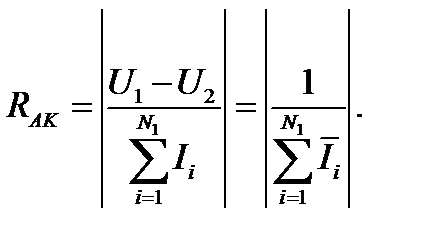(4.19)

Cпособ 2. В системе (4.17) выберем «опорный» электрод, на­пример, последний, с номером N, и соответствующее уравнение вычтем последовательно из всех остальных, а недостающее уравнение дополним условием электронейтральности:

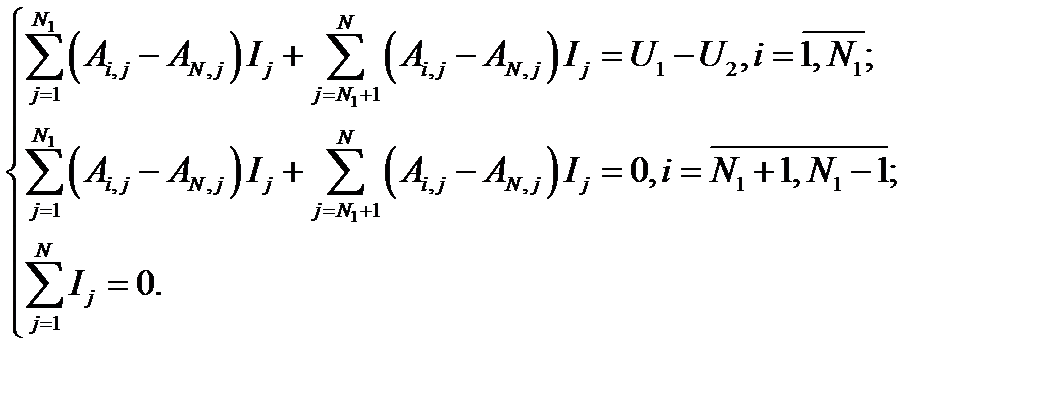
После деления всех уравнений на(U₁-U₂) получим СЛАУ размером N x N относительно приведенных значений токов 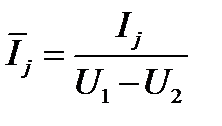. Сопротивление растеканию определяется по формуле (4.19).

Наиболее простой вид формулы для расчёта сопротивления растеканию между анодной и катодной секциями можно получить, если допустить равенство анодных токов субэлектродов I_i = I_A, (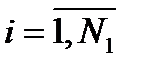) и равенство между собой катодных токов суб­электродов I_i = I_A, 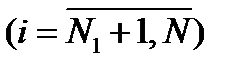. Тогда (4.17) запишется в виде

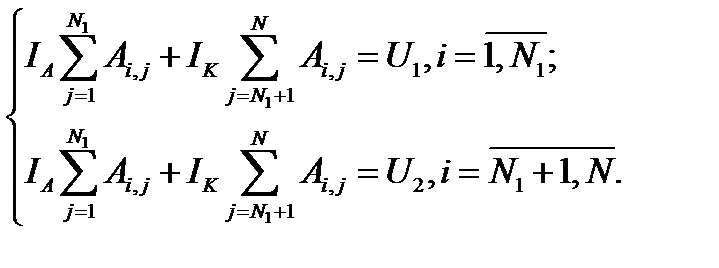
Решение поставленной задачи найдём методом граничных интегральных уравнений, которое может быть построено, напри­мер, с помощью потенциала простого электрического слоя. Об­щепринятые расчётные схемы решения интегральных уравнений позволяют свести их к системам линейных алгебраических урав­нений (СЛАУ).

В случае пластинчатых электродов соответствующая СЛАУ имеет вид [18]

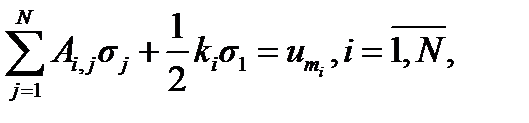(4.20)

а для тонких стержневых систем [14]:

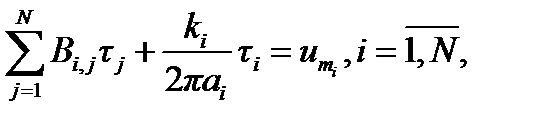(4.21)

где N — количество элементов, на которое разбивается поверх­ность электрода;

σ_i — безразмерная поверхностная плотность простого электрического слоя на i- м элементе;

τ_i — безразмерная линейная плотность простого электрического слоя, размещённого на осевой линии i -го элемента;

а_i — безразмерный радиус i -го элемента;

A_i,j,B_i,j — безразмерные потенциальные коэффици­енты.

Вид потенциальных коэффициентов зависит от структуры ок­ружающей среды, взаимного расположения i -го и j -го элемен­тов и метода решения интегрального уравнения. В случае одно­родной среды и применении метода Крылова-Боголюбова

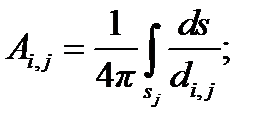
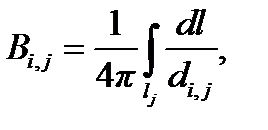
а при использовании метода подобластей

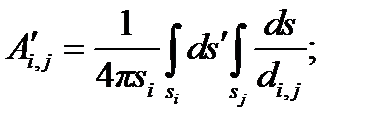
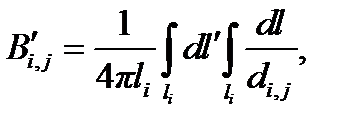
где s_i и l_i — соответственно безразмерные площадь и длина i -го элемента;

d_i,j — безразмерное расстояние между i -м и j -м эле­ментами.

Для эквипотенциального электрода (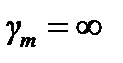) в правой части уравнений (4.20) и (4.21) u_mi = 1 для всех 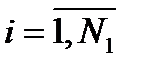, поэтому можно ввести понятие сопротивления растеканию электрода:

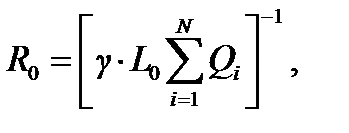(422)

где Q_i = σ_i s_i — для пластинчатых электродов и

Q_i = τ_i l_i — для стержневых электродов.

При наличии падения напряжения внутри электрода (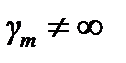) определение σ_i или τ_i непосредственно из (4.20) или (4.21) не­возможно, так как неизвестно распределение потенциала метал­ла u_m (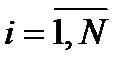). Однако с помощью СЛАУ вида (4.20) или (4.21) могут быть определены параметры эквивалентной электрической схемы замещения электродной системы, после чего методами теории линейных электрических цепей найдено и распределение потенциала металла.

Прямой (одношаговый) метод расчёта основан на построении полной электрической схемы замещения электрода. Поясним по­строение такой схемы для электрода в форме тонкого металли­ческого стержня длиной l с одним токовводом, для которого дос­таточно учитывать падение напряжения только по его длине (рис. 4.32).

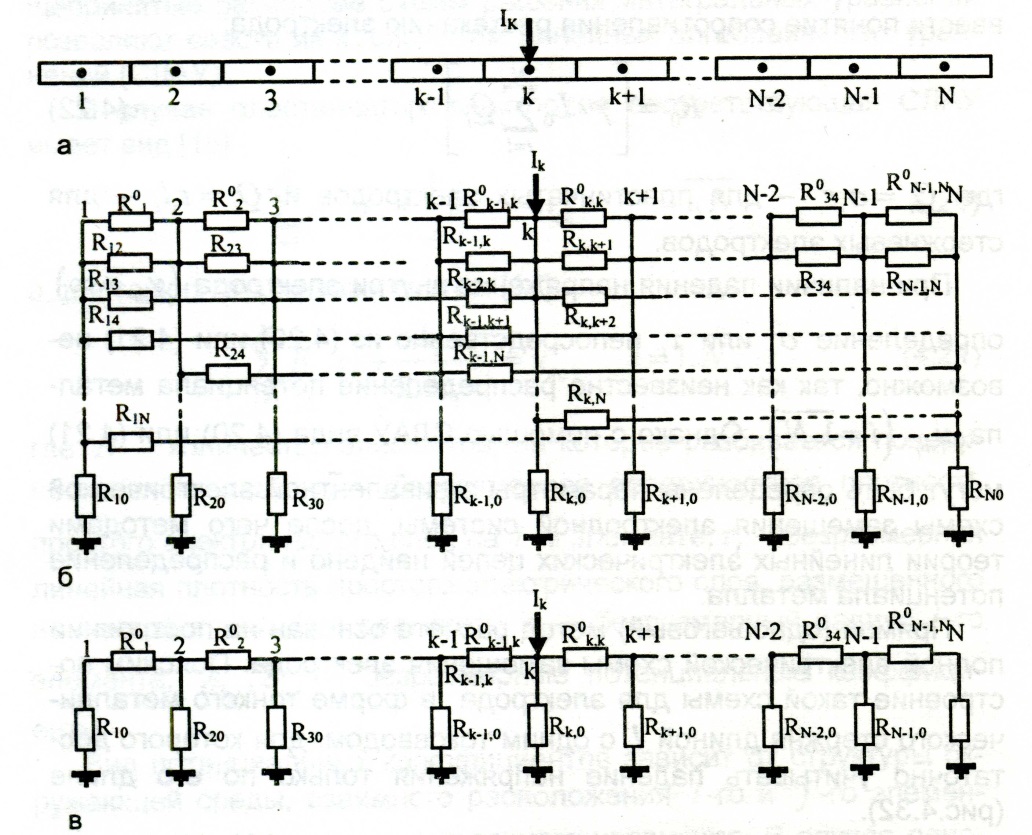
Рис.4.32. Протяжённый электрод с локальным подключением тока:

а - разбиение электрода на элементы; б - полная электрическая схема замещения электрода; в - частичная электрическая схема замещения электрода

После разбиения электрода по длине на N элементов 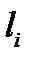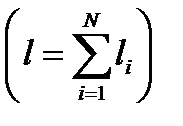выберем в геометрическом центре каждого элемента характерную точку, потенциал в которой примем за среднее зна­чение потенциала этого элемента. Полученную совокупность N субэлектродов будем считать многоэлектродной системой. Пусть в характерной точке k -го элемента вводится ток I_k (рис. 4.32, а).Тогда в соответствии с теорией многоэлектродных систем [6] полная эквивалентная электрическая схема замещения будет иметь вид, показанный на рис. 4.32, б, где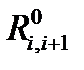 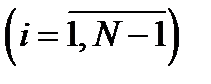— внутренние сопротивления схемы замещения;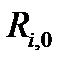 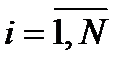и 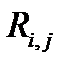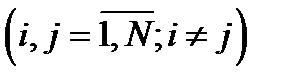— соответственно, собственные и взаимные частичные внешние сопротивления схемы замещения.

При известных параметрах полной схемы замещения неэквипотенциального электрода связь подводимых токов и потенциа­лов в характерных точках элементов определяется методом уз­ловых напряжений и в матричной форме имеет вид

GX = Y, (4.23)

где для схемы замещения, соответствующей рис. 4.32, б матрица проводимостей имеет вид

g₁₁ ‒ g_12. ‒ g_1,k-1 0 ‒ g_1,k+1 . ‒ g_1,N-1 ‒ g_1,N

‒ g₂₁ g₂₂. ‒ g_2,k-1 0 ‒ g_2,k+1. ‒ g_2,N-1 ‒ g_2,N

_.. .....

‒ g_k-1,1 ‒ g_k-1,2. g_k-1,k-1 0 ‒ g_k-1,k+1. ‒ g_k-1,N-1 ‒ g_k-1,N

G = ‒ g_k,1 ‒ g_k,2 . ‒ g_k,k-1 0 ‒ g_k,k+1. ‒ g_k,N-1 ‒ g_k,N

‒ g_k+1,1 ‒ g_k+1,2. ‒ g_k+1,K-1 0 g_k+1,k+1. ‒ g_k+1,N-1 ‒ g_k+1,N

_.......

‒ g_N-1,1 ‒ g_N-1,2. ‒ g_N-1,k-1 0 ‒ g_N-1,k+1. g_N-1,N-1 ‒ g_N-1,N

‒ g_N,1 ‒ g_N,2 . ‒ g_N,k-1 0 ‒ g_N,k+1. ‒ g_N,N-1 g_N,N

u₁ 0

u₂ .

. 0

u_k-1; Y = g_k-1,k.

X = J_k ‒ g_k,k

u_k+1 g_k+1,k

. 0

u_N-1 .

u_N 0

u_i = U_i / U_k — безразмерное напряжение между i -м узлом (харак­терной точкой элемента) и бесконечностью;

U_k=U₀ – масштаб потенциала (потенциал в месте токоввода);

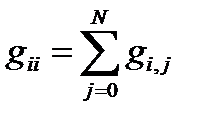— сумма безразмерных полных проводимостей всех ветвей, сходящихся в i -м узле;

g_i,j (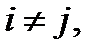 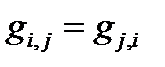) — безразмерная полная проводи­мость ветвей, соединяющих i -м и j- м узлы;

J _k — безразмерный ток, который вводится в узел с номером k.

В частности, для схемы замещения стержневого электрода, приведённой на рис. 4.32, б:

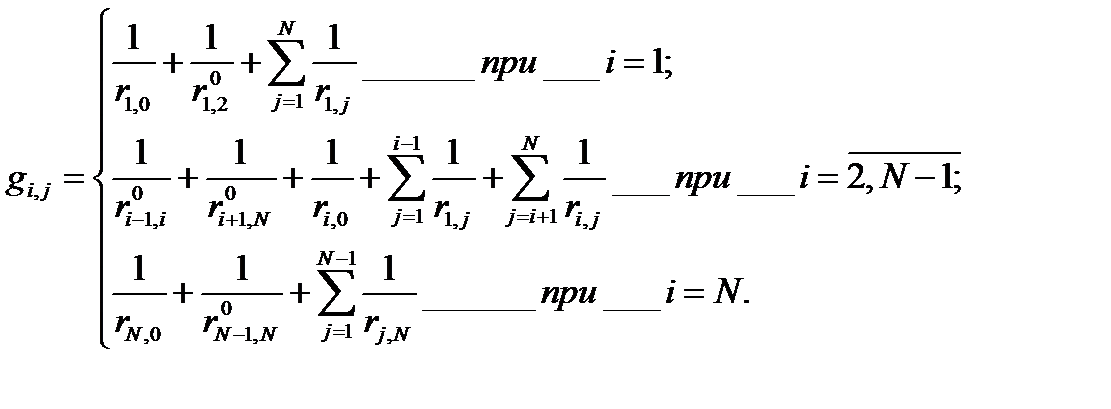(4.24)

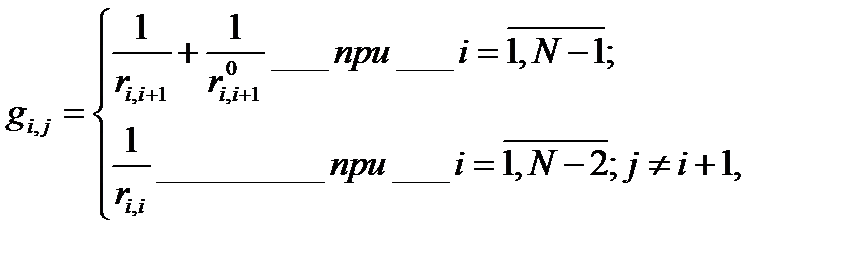(4.25)

где 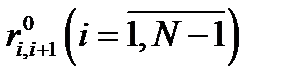— внутренние безразмерные сопротивления схемы замещения;

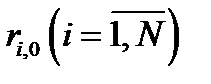и 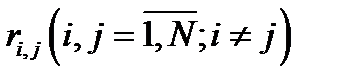— соответ­ственно собственные и взаимные частичные внешние безразмер­ные сопротивления схемы замещения.

Для неэквипотенциальных электродных систем определяют входное сопротивление по формуле

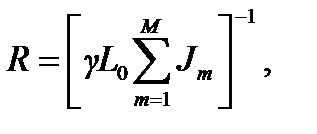(4.26)

где M — количество токовводов.

Отметим, что при М = N значения сопротивлений по форму­лам (4.22) и (4.26) совпадают.

Для нахождения всех собственных частичных сопротивлений эквивалентной схемы замещения для стержневой электродной системы находится решение СЛАУ вида

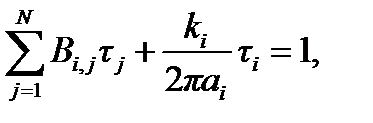
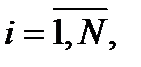(4.27)

после чего

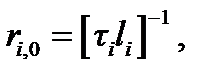
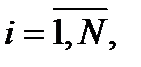(4.28)

Для определения всех взаимных частичных сопротивлений стержневой электродной системы решается СЛАУ вида

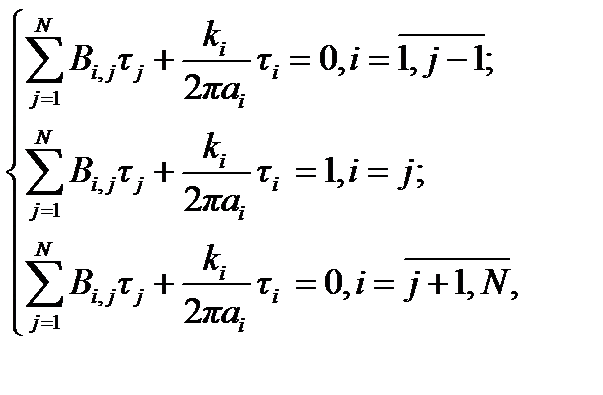(4.29)

а значения r_{i, j} определяется по формуле

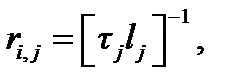
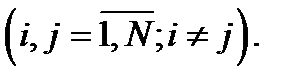(4.30)

Внутренние сопротивления схемы замещения рассчитывают­ся по формуле

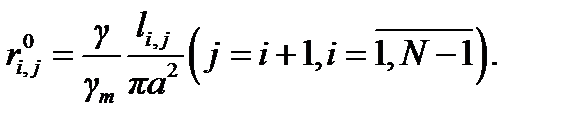(4.31)

где l_i,j — безразмерное расстояние между характерными точками соседних элементов.

Для пластинчатых электродных систем собственные и взаим­ные частичные сопротивления определяются из соотношений (4.27)‒(4.31) с заменой B_i,j на A_i,j, τ_j на σ_j, l_j на s_j и 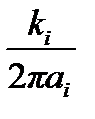на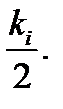

В теории неэквипотенциальных заземлителей широко приме­няется итерационный (многошаговый) метод, при реализации ко­торого используется упрощённая электрическая схема замещения электрода без учёта взаимных частичных сопротивлений. Для стержневого электрода такая схема показана на рис. 4.32, в. При этом матрица G имеет вид

g₁₁ ‒ g₁₂ 0...._. 0

‒ g₂₁ g₂₂ ‒ g₂₁ 0.....

_.. .......

0. ‒ g_k-1,k-2 g_k-1,k-1 0 0.. 0

G = 0. 0 ‒ g_k,k-1 ‒ 1 ‒ g_k,k+1 0. 0

0_...... 0 0

_.........

0.... 0 ‒ g_N-1,N-2 g_N-1,N-1 ‒ g_N-1,N

0..... 0 ‒ g_N,N-1 g_N,N

где

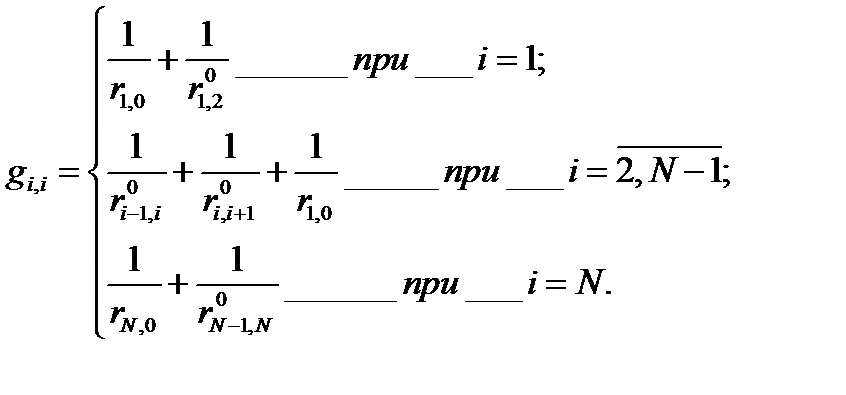(4.32)

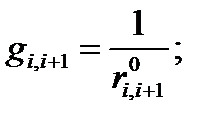
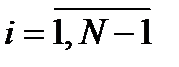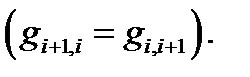, (4.33)

Алгоритм итерационного метода для стержневого электрода состоит из следующих шагов.

Решая СЛАУ (4.27), определяют начальные значения r_i0 из (4.29).

Рассчитывают полные проводимости g_i,j из (4.32), (4.33) и находят узловые потенциалы u_i (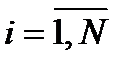) из (4.23) с учётом вида матрицы G.

Решают СЛАУ (4.27) с правой частью, где вместо 1 подстав­ляют u_i (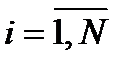), и определяют новые значения собственных частичных сопротивлений по формуле

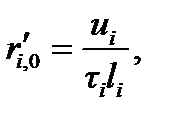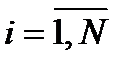(). (4.34)

Определяют новые полные проводимости g_i,j из (4.32), (4.33) и находят новые значения узловых потенциалов u_i (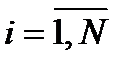) из (4.23) с учётом вида матрицы G.

Данный процесс продолжается до тех пор, пока на п -м шаге итерации

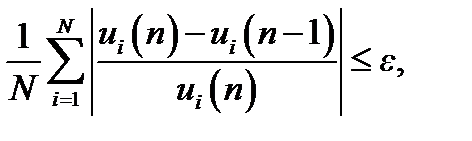
где ε — заданная погрешность расчёта.

Пример 4.9. Рассмотрим стержневой электрод длиной L₀ = 300 м, с наружным диаметром D = 0.05 м. Материал электро­да — сталь с удельной электропроводимостью у_т = 7 10⁶ См/м, внешняя среда — морская вода с удельной электропроводимостью 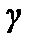= 3 См/м. Электрод разобьём на 300 (N) равных элементов. За масштаб потенциала примем потенциал первого элемента (U₀ = U₁), в который водится ток I₁.

Потенциальные коэффициенты находятся по формуле

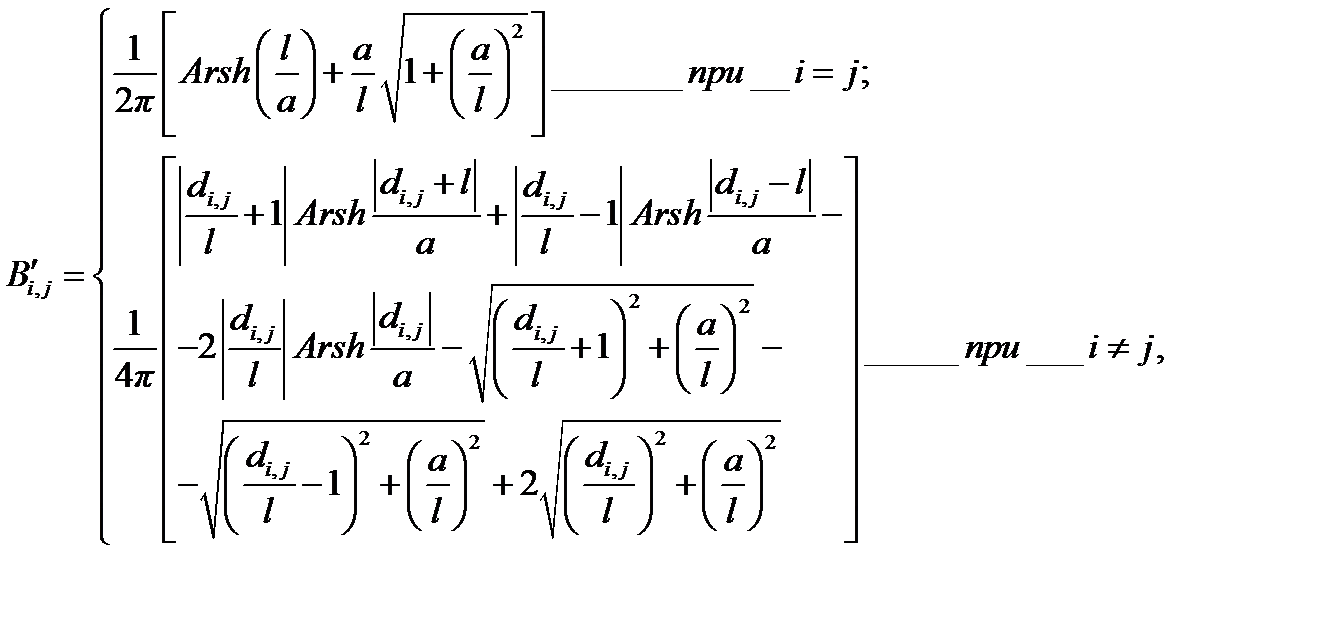
где l — длина одного элемента;

а — радиус электрода;

d_i,j — рас­стояние между центрами i -го и j -го элементов.

Результаты расчёта прямым и итерационным методом пред­ставлены в табл. 4.2. Погрешность итерационного метода составляла ε = 0.0005, а поверхностное сопротивление не учитыва­лось.

Таблица 4.2