Симметризация — это такое геометрическое преобразование объёмного или плоского тела, которое позволяет привести его к виду, симметричному относительно некоторой плоскости (плоская симметризация) или оси (осевая симметризация). При плоской симметризации (рис.4.23, а) через каждую точку поверхности тела А проводят прямые перпендикулярные плоскости Р, откладывают на этих прямых симметрично относительно плоскости Р отрезки, равные длинам хорд, высекаемых на рассматриваемой прямой телом А (L1, L2, L3,...).
Геометрическое место концов таких отрезков образует поверхность нового тела А', симметричного относительно плоскости Р. Аналогично выполняется симметризация пластины относительно прямой, лежащей в её плоскости.
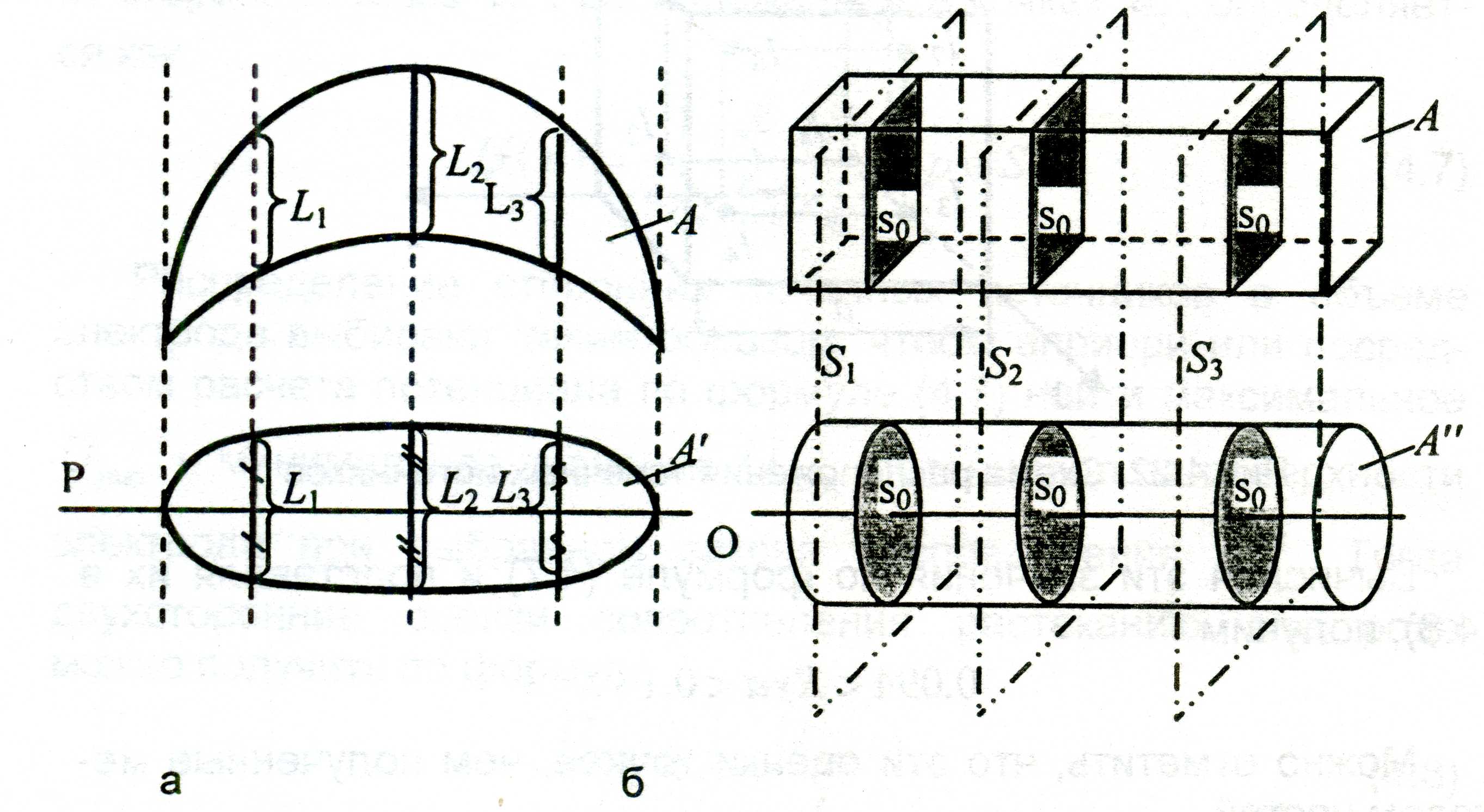
Рис.4.23. Построение плоской и осевой симметризации
При осевой симметризации объёмного тела относительно оси 0 (на рис.4.23, б таким телом является параллелепипед) через тело А проводят плоскости (S1, S2, S3,....), перпендикулярные оси 0, и строят в каждой из них диск с центром на оси 0, равновеликий по площади сечению (s0), которое высекает тело А на соответствующей плоскости S. Геометрическое место периметров таких окружностей образует новое тело А", симметричное относительно оси 0.
Свойства симметризации
1. При симметризации пластин относительно плоскости их площадь остаётся неизменной.
2. При любом виде симметризации объёмного тела его объём остаётся неизменным.
3. При бесконечном числе симметризаций любая пластина переходит в диск той же площади.
4. При бесконечном числе симметризаций любое объёмное тело переходит в сферу того же объёма.
5. При любом виде симметризаций сопротивление растеканию, по крайней мере, не уменьшается.
Поскольку любая пластина при бесконечном числе симметризаций (различно ориентированных относительно её плоскостей) переходит в равновеликий диск, для её сопротивления растеканию можно дать верхнюю оценку через её площадь Sпл, используя известное значение сопротивления дискового электрода, радиус которого 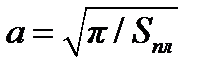 , по формуле
, по формуле
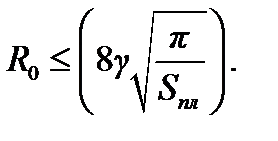 (4.9)
(4.9)
Знак равенства в (4.9) достигается только в том случае, если исходная пластина имела форму диска.
Для сопротивления растеканию объёмного тела можно получить верхнюю оценку через его объём VT, используя известное выражение для сопротивления сферы того же объёма радиусом 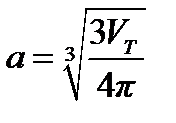 , а именно:
, а именно:
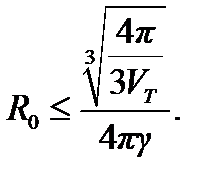 (4.10)
(4.10)
Знак равенства в (4.10) достигается только в том случае, если исходное тело имело форму сферы.
Пример 4.6. Оценим по методу симметризации сопротивление растекания электродов в форме квадратной пластины и куба. Из (4.9) получим, что для квадратной пластины со стороной а R0γa < 0.2216, а для куба с ребром а из (4.10) получим R0γa < 0.1283.
4.3.4. Метод средних потенциалов (метод Хоу)
Метод основан на замене электрода средой, имеющей ту же форму, что и рассматриваемый электрод, и ту же электропроводимость, что и окружающая среда. При этом вместо неизвестного истинного распределения плотности тока на поверхности электрода задаётся некоторое фиктивное распределение сторонних точечных источников тока σст (S). В случае тонких стержневых электродов, для которых можно пренебречь неравномерностью распределения плотности тока вдоль образующей их поперечного сечения, на их оси задаётся фиктивное линейное распределение сторонних точечных источников τст (l). При этом в силу принципа непрерывности тока полный ток через поверхность, совпадающую с поверхностью электрода в зависимости от выбранного распределения сторонних источников тока, определяется как
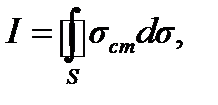
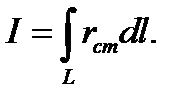
Потенциал в произвольной точке р поверхности электрода определяется при этом из формул
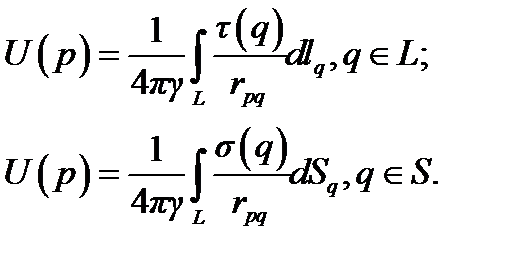
Если выбранное распределение сторонних фиктивных точечных источников приводит к распределению тока на поверхности электрода, отличному от истинного (равновесного), то поверхность рассматриваемого электрода оказывается неэквипотенциапьной. Чтобы избежать неоднозначности в выборе потенциала, на всей поверхности электрода принимается постоянное значение, равное среднему арифметическому значений потенциала во всех точках поверхности тела S:
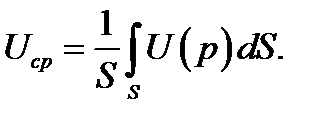
Для стержневых электродов в силу постоянства потенциала в каждом сечении вдоль образующей среднее значение потенциала определяется по формуле
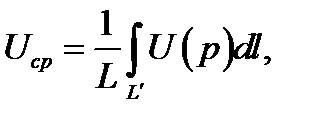
где L' — линия, параллельная осевой линии стержневого электрода и принадлежащая его поверхности.
Сопротивление растеканию определяется по формуле
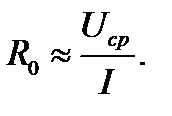 (4.11)
(4.11)
Поскольку сопротивление растеканию является интегральной характеристикой электрического поля, закон распределения сторонних фиктивных точечных источников тока мало влияет на точность расчёта по формуле (4.11). Наиболее простая схема расчёта (предложенная в своё время Г. Хоу и носящая его имя) основана на задании равномерного распределения сторонних источников по поверхности электрода <тст(5) = //5 или вдоль осевых линий стержневых электродов τст (l) = I / L.
Тогда выражения для расчёта сопротивления растеканию электрода по методу Хоу принимает вид:
- для объёмных и пластинчатых электродов
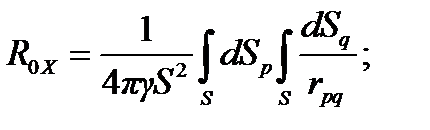 (4 12)
(4 12)
- для стержневых электродов
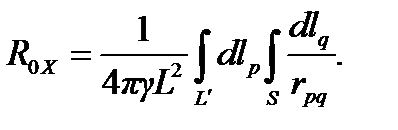 (4.13)
(4.13)
Поскольку равновесное (истинное) распределение плотности тока на поверхности электрода соответствует минимуму энергии электрического поля, значение сопротивления растеканию, найденное методом средних потенциалов (в частности, и методом Хоу), всегда больше истинного значения сопротивления, за исключением тех случаев, когда выбранное фиктивное распределение тока совпадает с истинным (в методе Хоу — для электрода сферической формы).
Например, верхняя оценка сопротивления для куба с ребром а по методу Хоу R0γa < 0.1226.
При расчёте сопротивления растеканию между двумя электродами средний потенциал каждого из них определяется с учётом, что 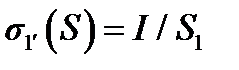 , a
, a 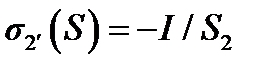 (где I — полный ток одного из электродов), по формулам
(где I — полный ток одного из электродов), по формулам
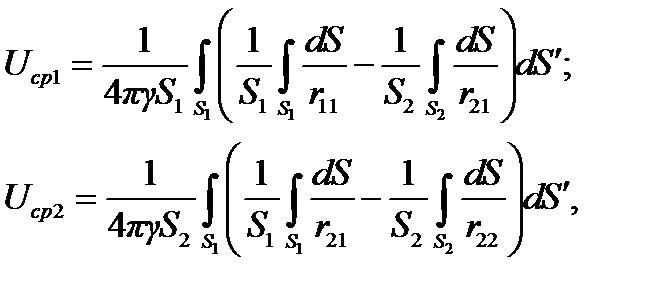
где S1 и S2 — поверхности электродов;
r11, r22 — расстояние между двумя произвольными точками поверхности одного и того же электрода;
r12 = r21 — расстояние между двумя произвольными точками, принадлежащими разным электродам.
Сопротивление растеканию определяется по формуле
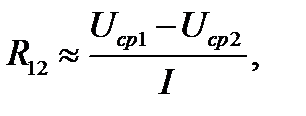
или с учётом
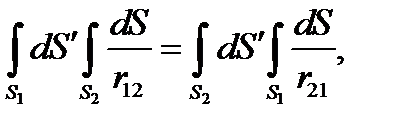
имеем
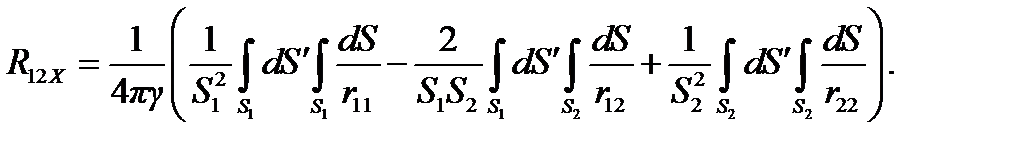 (4.14)
(4.14)
Для сопротивления растеканию между двумя стержневыми электродами с длинами L1 и L2 аналогично получим:
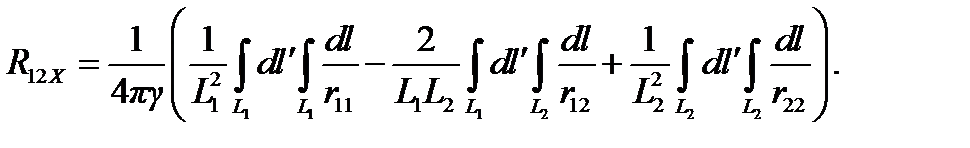 (4.15)
(4.15)
Нетрудно видеть, что первое и третье слагаемые в (4.14) и (4.15) представляют собой сопротивления растеканию уединённых электродов R10X и R20X, вычисленных методом Хоу. Двойной интеграл во втором слагаемом в (4.14) и (4.15) при условии, что расстояние между электродами в несколько раз превышает их габаритные максимальные размеры, принимает вид 2S1S2 / rср (или 2L1L2 / rср), где rср — среднее расстояние между точками поверхности электродов 1 и 2. Тогда формулы (4.14) и (4.15) запишутся так:
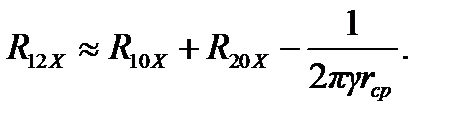
Другие вопросы применения метода средних потенциалов приведены в [9].
Пример 4.7. Сопротивление растеканию прямоугольной пластины размером а х b. В соответствии с обозначениями, показанными на рис. 4.24, двойной поверхностный интеграл, входящий в (4.12), будет
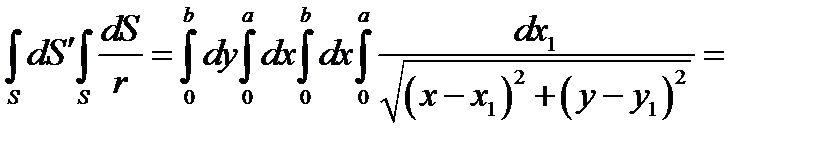
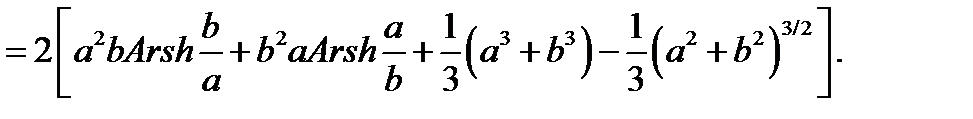
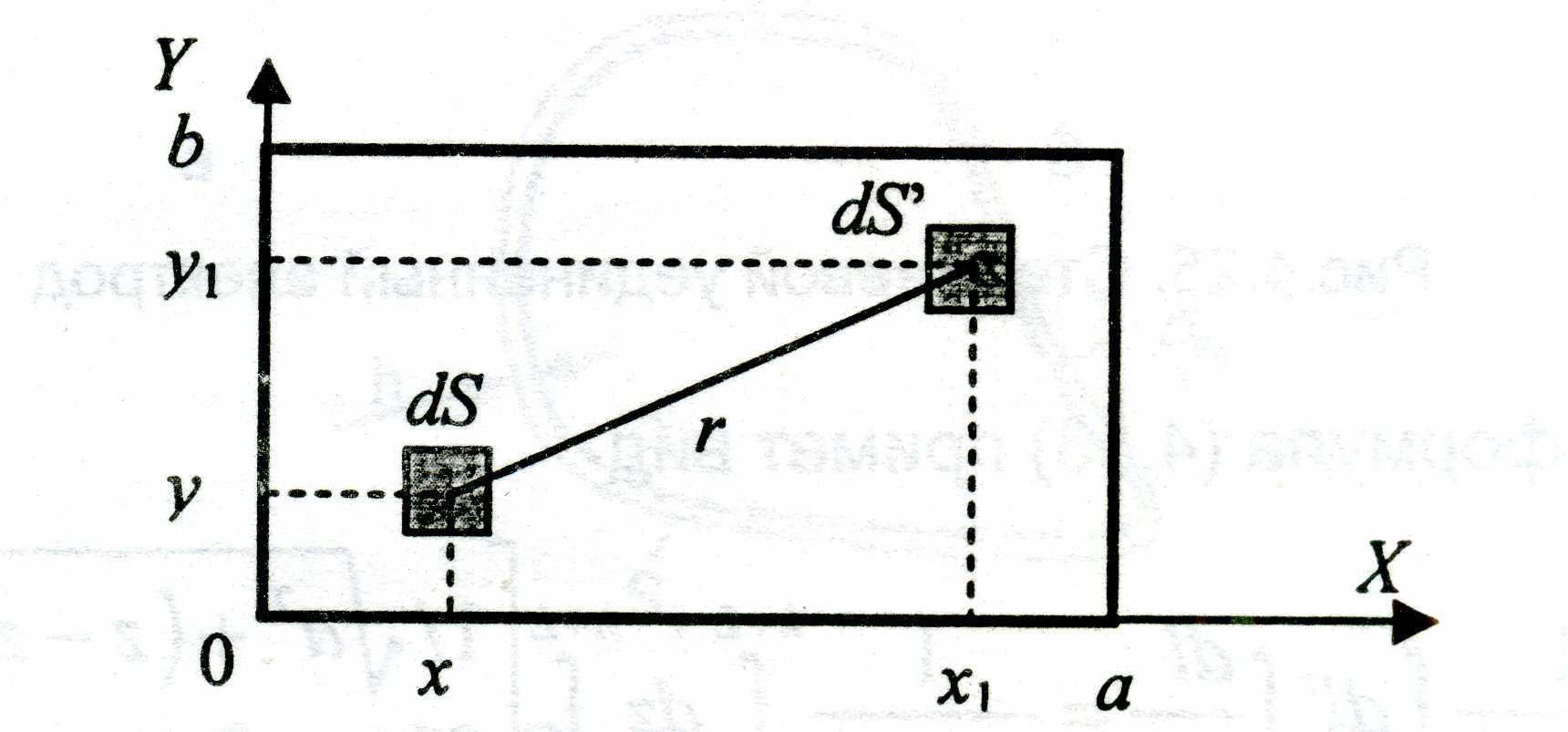
Рис. 4.24. К вычислению среднего потенциала
Окончательно для сопротивления растеканию прямоугольной пластины по методу Хоу получим
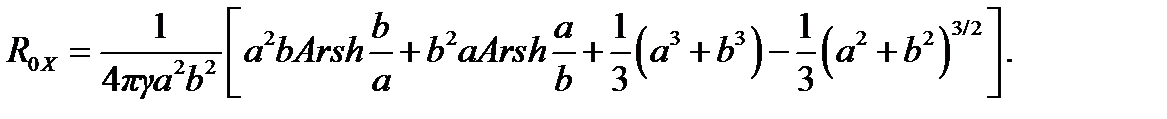
В частном случае квадратной пластины со стороной а
R0X  γ а = 0.2366.
γ а = 0.2366.
Пример 4.8. Сопротивление растеканию вертикального стержневого электрода, заглублённого относительно границы раздела вода-воздух (рис. 4.25, а).
В соответствии с методом Хоу заменим стержневой электрод линейным распределением τ сторонних точечных источников тока (рис. 4.25, б), а границу раздела вода-воздух учтём зеркальным отражением этих источников (рис.4.25, в).
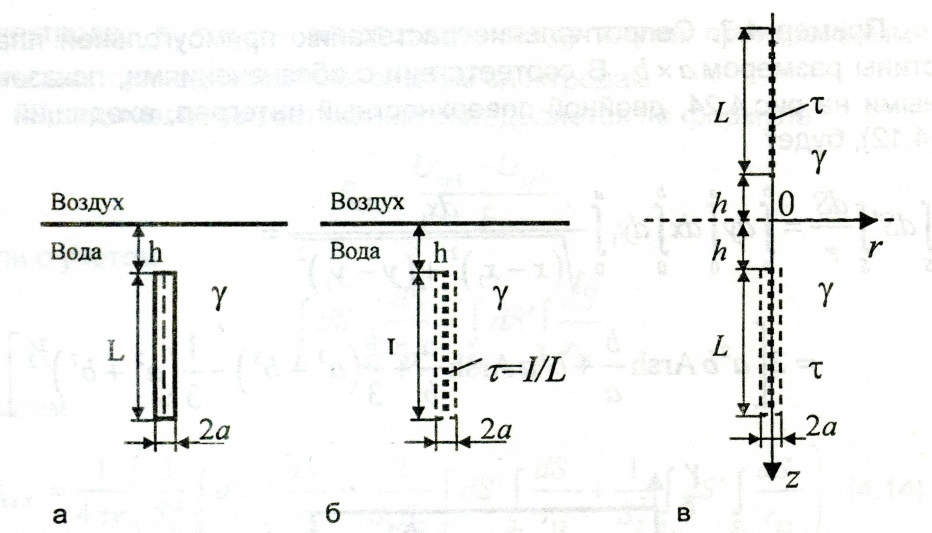
Рис. 4.25. Стержневой уединённый электрод
Тогда формула (4.13) примет вид
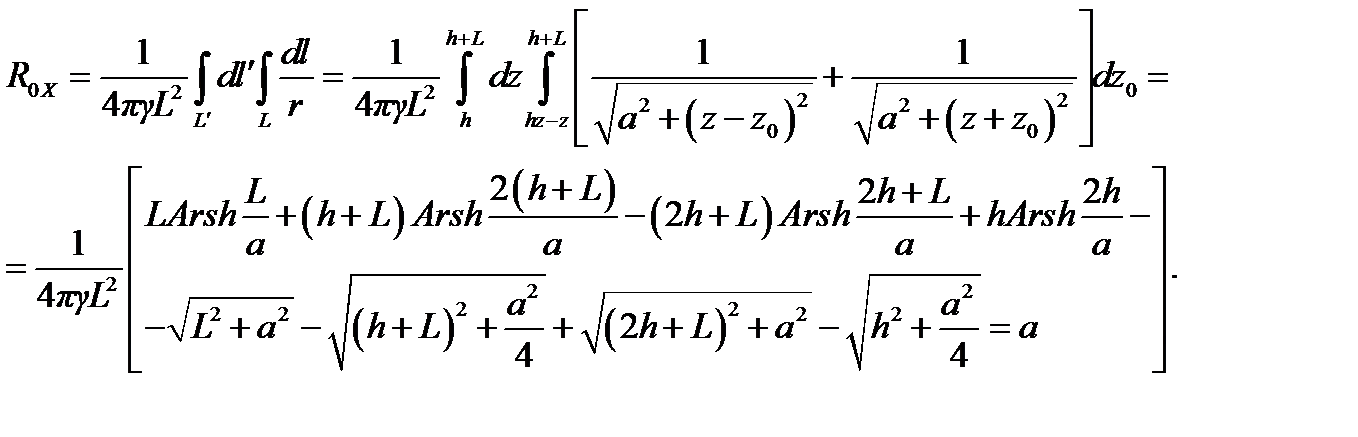
При 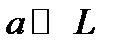 и
и  формула упрощается:
формула упрощается:
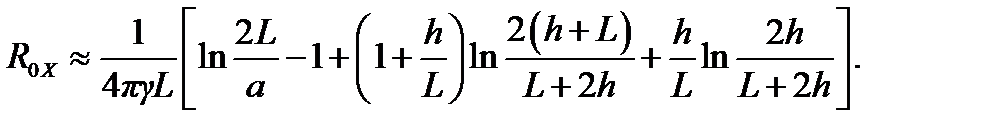
 2015-08-21
2015-08-21 982
982








