2015-08-12
378
Введем случайную величину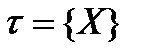 
, где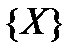 
обозначает дробную часть величины Х. Теперь продолжительность жизни Х можно представить суммой целой и дробной частей: 
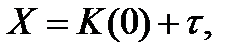где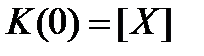 
- округление время жизни. Понятно, что величина 
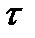описывает момент смерти внутри года. Найдем уравнение распределения 
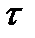при условии, что смерть наступила в возрасте n лет:
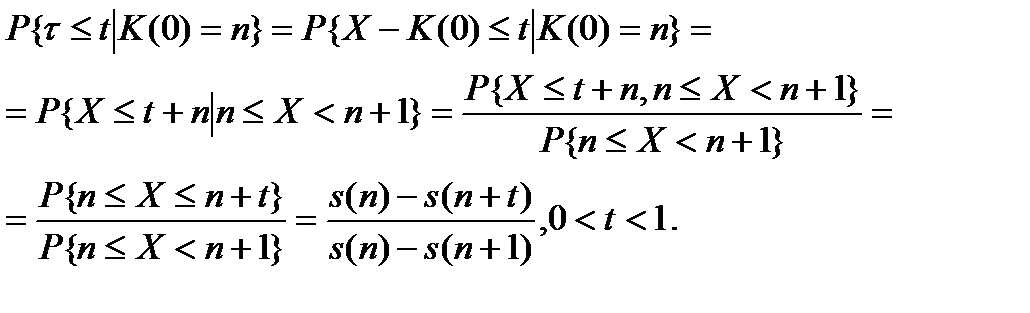(2.2.1)
Величины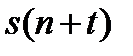 
, точнее 
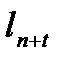, когда 
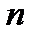-целое, а 
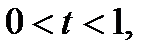в ТПЖ отсутствует, поэтому при ее нахождении воспользуемся приближениями для дробных возрастов.
При постулате равномерного распределения смертей формула (2.2.1), если взять в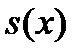 
аргумент 
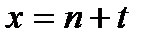, преобразуется следующим образом:
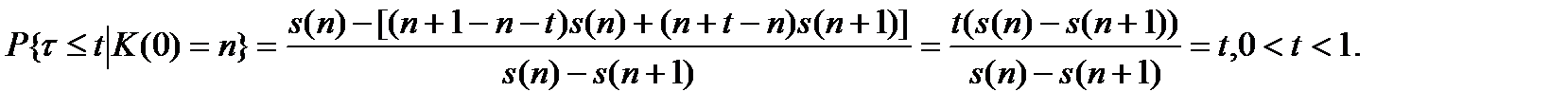
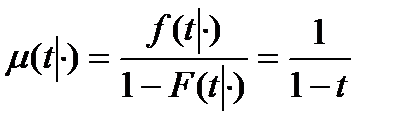
Итак, при этой интерполяции:
1. Смерть в любой день между двумя днями рождений человека равновероятна;
2. Условное распределение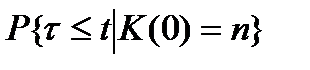 
не зависит от 
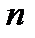и поэтому совпадает с безусловным распределением 
;
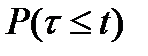3. Случайные величины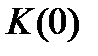 
и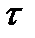 
независимы.
Для постулата постоянной интенсивности смертности аналогично имеем:
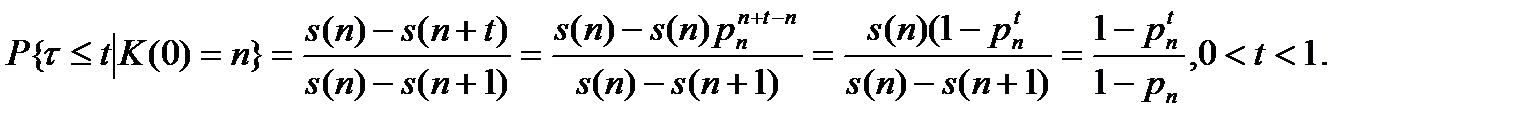
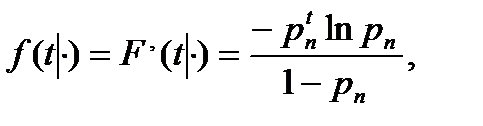
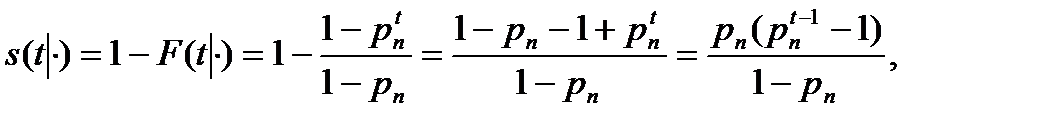
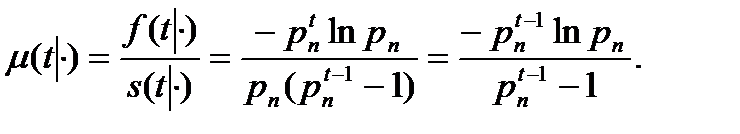
Рассуждая аналогично, также можно получить формулы для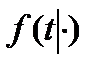 
, 
, 
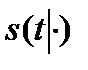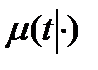и при постулате Балдуччи.
Замечание. Вообще говоря, формулы при постоянной интенсивности смертности удобнее выразить через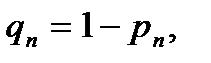 
так как величина 
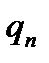имеется в ТПЖ.
