2015-08-12
401
Обучение в университете длится 4 года. Из поступивших студентов на 1 курс специальности математика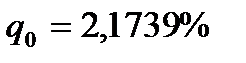 
(по разным причинам) не переходят на 2 курс. Из начавших обучение на 2, 3, 4 курсах 
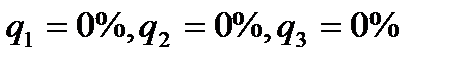не заканчивают соответствующий курс. Предполагая, что внутри года момент ухода имеет равномерное распределение, мы найдем среднее время, которое студент, поступивший на 1 курс, проведет в университете на протяжении ближайших 2,5 лет.
Решение:
В актуарных обозначениях, искомая величина это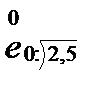 
. Как известно,
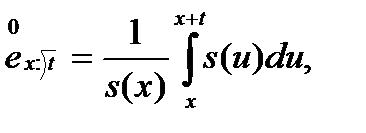
где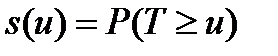 
и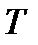 
- момент ухода из университета. Поскольку 
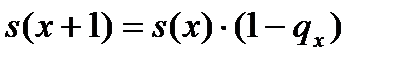и 
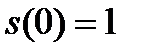, можно подсчитать 
:
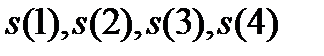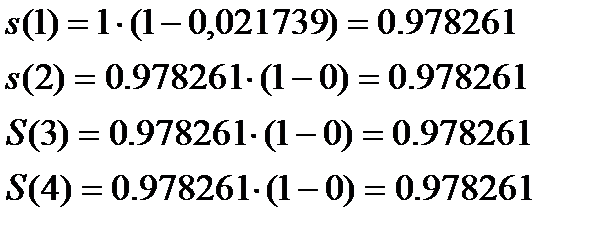
Предположение о равномерном распределении ухода внутри академического года означает линейную интерполяцию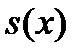 
для нецелых значений 
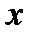. Поэтому
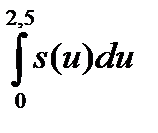
Можно найти как сумму площадей двух трапеций.
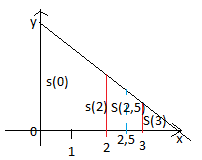
Первая трапеция имеет основания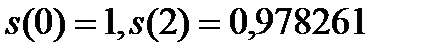 
и высоту 2. Вторая трапеция имеет основания 
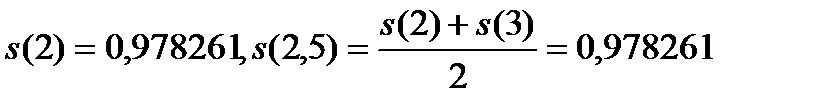и высоту 0,5.
Вычисляем площадь трапеции по формуле:
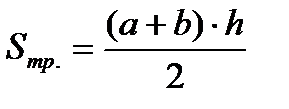
следовательно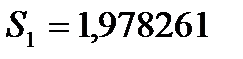 
, а 
.
Поэтому
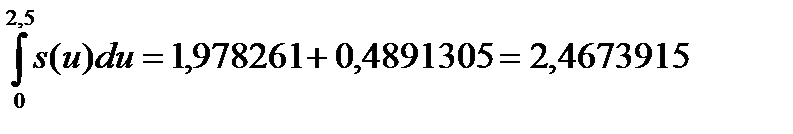
и, значит,
.
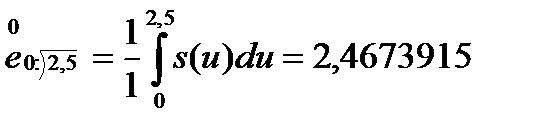Аналогично вычисляем среднее время которое студенты специальностей информатика, ИС и ВТиПО, поступившие на 1 курс, проведут в университете на протяжении ближайших 2,5 лет.
Специальноть-информатика
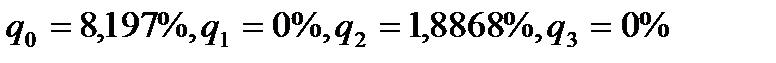
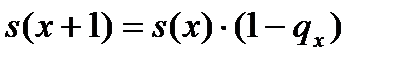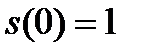Поскольку и , можно подсчитать :
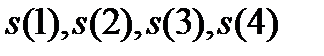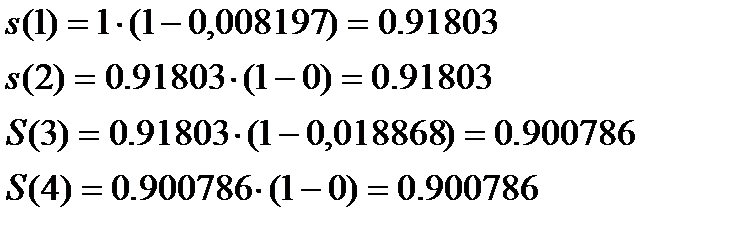
Предположение о равномерном распределении ухода внутри академического года означает линейную интерполяцию 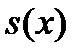для нецелых значений 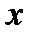. Поэтому
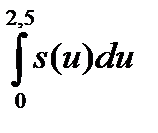
Можно найти как сумму площадей двух трапеций.
Первая трапеция имеет основания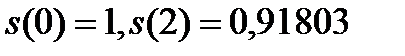 
и высоту 2. Вторая трапеция имеет основания 
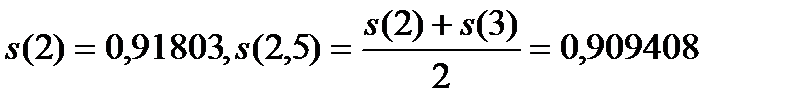и высоту 0,5.
Вычисляем площадь трапеции по формуле:
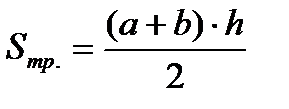
следовательно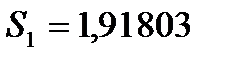 
, а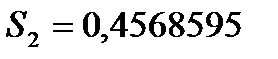 
.
Поэтому
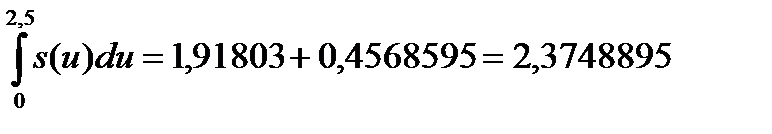
и, значит,
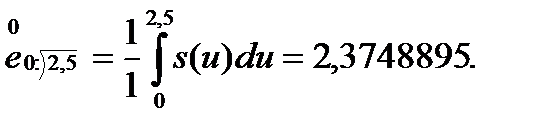
Специальноть-информационные системы
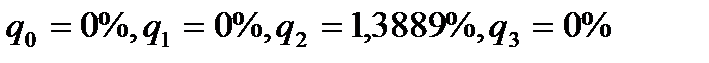
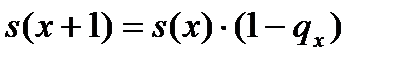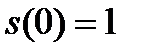Поскольку и , можно подсчитать :
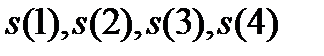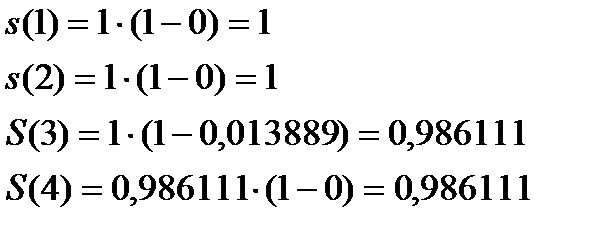
Предположение о равномерном распределении ухода внутри академического года означает линейную интерполяцию 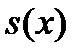для нецелых значений 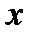. Поэтому
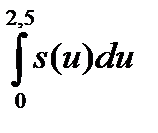
Можно найти как сумму площадей двух трапеций.
Первая трапеция имеет основания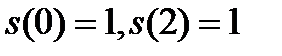 
и высоту 2. Вторая трапеция имеет основания 
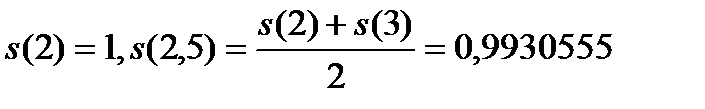и высоту 0,5.
Вычисляем площадь трапеции по формуле:
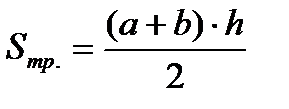
следовательно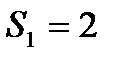 
, а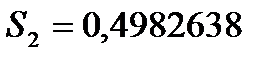 
.
Поэтому
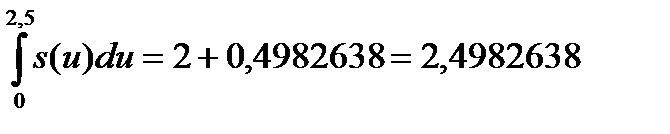
и, значит,
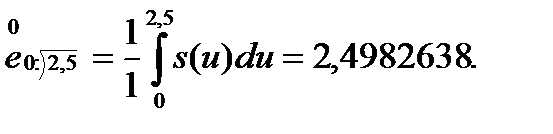
Специальность-ВТиПО
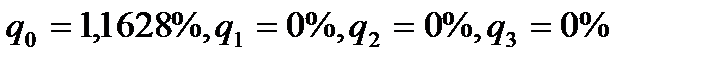
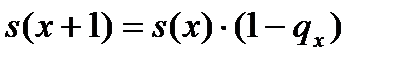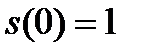Поскольку и , можно подсчитать :
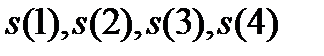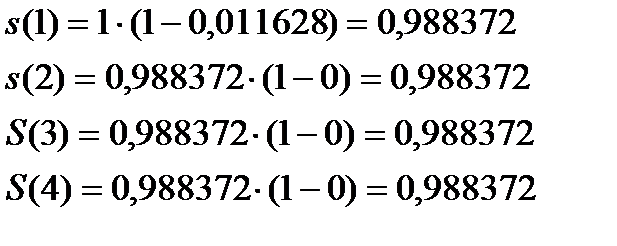
Предположение о равномерном распределении ухода внутри академического года означает линейную интерполяцию 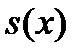для нецелых значений 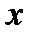. Поэтому
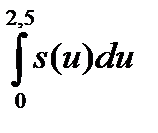
Можно найти как сумму площадей двух трапеций.
Первая трапеция имеет основания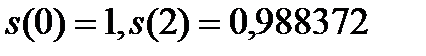 
и высоту 2. Вторая трапеция имеет основания 
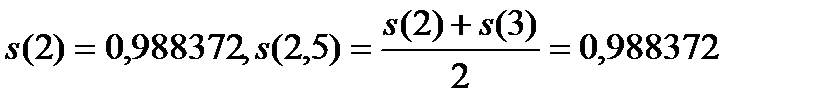и высоту 0,5.
Вычисляем площадь трапеции по формуле:
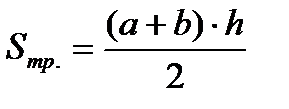
следовательно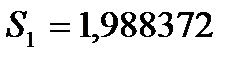 
, а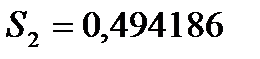 
.
Поэтому
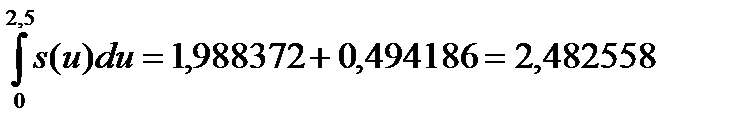
и, значит,
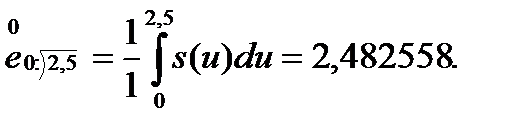
Вывод:
Исходя, от полученных результатов можно сделать вывод, что 1 место за самау высокую вероятность доучиться до 3 курса у студентов специальности информационные системы;
2-е место - студенты специальности – вычислительная техника и программное обеспечение;
3-е место - студенты специальности – математика;
4-е место - студенты специальности – информатика.
