Мы рассмотрим 3 широко используемых в актуарной науке предположения, так называемых сплайнов. Они будут сформулированы в терминах функции дожития и в такой форме, которая позволяет показать природу интерполяции на интервале (x,x+1), вытекающую из каждого из этих предположений. В каждом утверждении x является целым и 0≤t≤1. Сформулируем предположения:
· Линейная интерполяция: 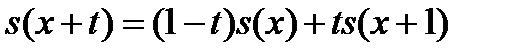 . Это приводит к равномерному распределению или, точнее, к равномерному распределению моментов смерти внутри каждого годичного возрастного интервала. При этом предположении
. Это приводит к равномерному распределению или, точнее, к равномерному распределению моментов смерти внутри каждого годичного возрастного интервала. При этом предположении 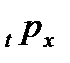 является линейной функцией.
является линейной функцией.
· Показательная интерполяция, или линейная интерполяция для 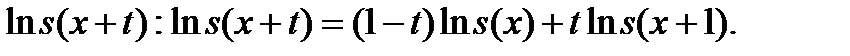 Это согласуется с предположением о постоянной интенсивности смертности внутри каждого годичного возрастного интервала. При этом предположении
Это согласуется с предположением о постоянной интенсивности смертности внутри каждого годичного возрастного интервала. При этом предположении 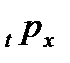 является показательной функцией.
является показательной функцией.
· Гармоническая интерполяция: 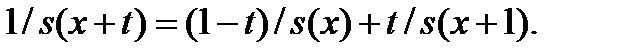 Это то, что называется предположением о гиперболичности (исторически, предположением
Это то, что называется предположением о гиперболичности (исторически, предположением 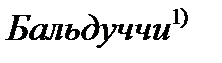 ), поскольку в этом случае
), поскольку в этом случае 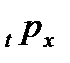 является гиперболической кривой.
является гиперболической кривой.
 предположение названо по имени Дж. Бальдуччи, итальянского актуария, который указал роль этого предположения в традиционном актуарном методе построения таблиц смертности.
предположение названо по имени Дж. Бальдуччи, итальянского актуария, который указал роль этого предположения в традиционном актуарном методе построения таблиц смертности.
Опираясь на эти основные определения, для остальных стандартных вероятностных функций можно вывести формулы в терминах вероятностей, указанных в табл. 1.
Вывод выражений, входящих в табл.1, является просто упражнением, заключающимся в подстановке сформулированных выше предположений о 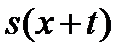 в соответствующие формулы. Мы продемонстрируем этот процесс для равномерного распределения смертей.
в соответствующие формулы. Мы продемонстрируем этот процесс для равномерного распределения смертей.
Для определения первого выражения в столбце, относящимся к равномерному распределению, начнем с соотношения
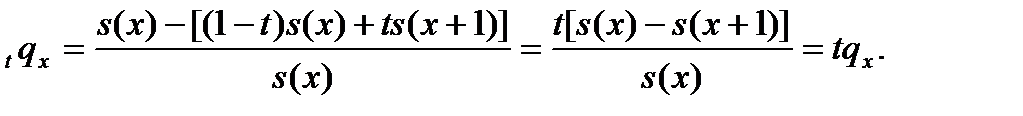
Для второго выражения воспользуемся формулой:
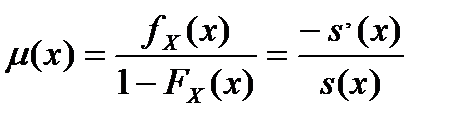 и
и
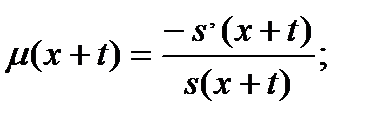
далее, подставляя соответствующие выражения для 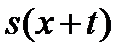 , получаем
, получаем
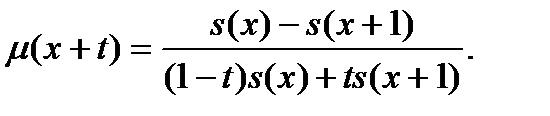
Деление числителя и знаменателя в правой части на 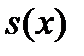 приводит к формуле
приводит к формуле
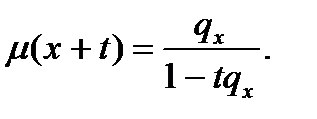
Третье выражение является частным случаем четвертого при 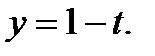 рассматривая четвертое выражение, начнем с равенства
рассматривая четвертое выражение, начнем с равенства
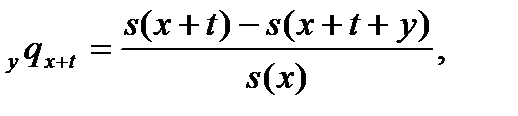
а затем, подставим соответствующее выражение для 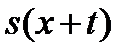 и
и 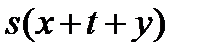 , получим
, получим
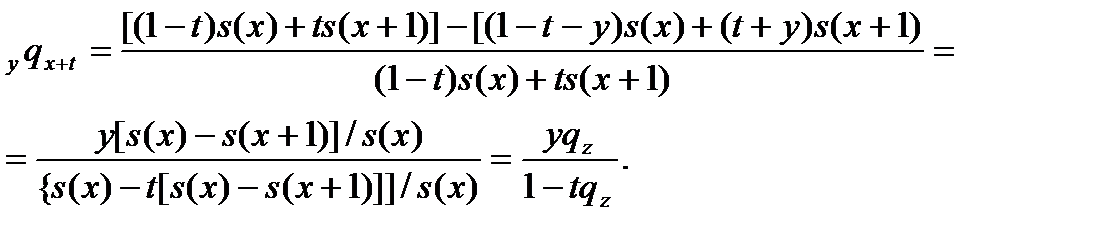
Пятое выражение является дополнением первого, и последнее выражение в столбце, относящемся к равномерному распределению, является произведением второго и пятого выражений.
Таблица 1.
Вероятностные функции для дробных возрастов 
| Функция | Предположения | ||
| Равномерное распределение | Постоянная интенсивность | Гиперболичность | |
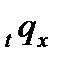 | 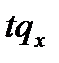 | 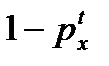 | 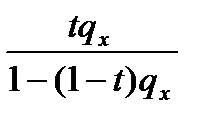 |
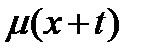 | 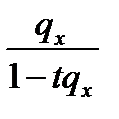 | 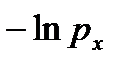 | 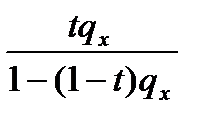 |
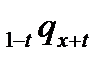 | 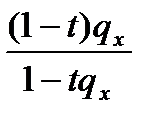 | 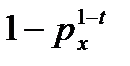 | 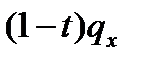 |
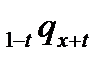 | 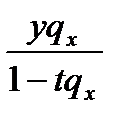 | 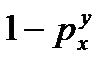 | 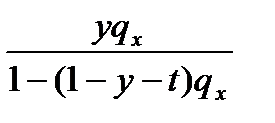 |
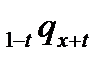 | 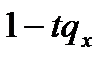 | 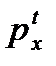 | 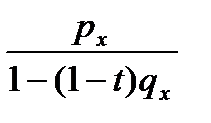 |
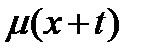 | 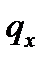 | 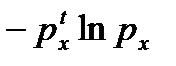 | 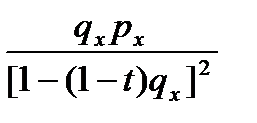 |
 , что в этой таблице
, что в этой таблице 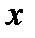 целое,
целое, 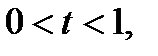
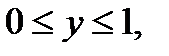
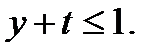 в первой, третьей, четвертой и пятой строках соотношения справедливы так же для
в первой, третьей, четвертой и пятой строках соотношения справедливы так же для 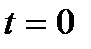 и
и 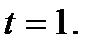
Если, как и ранее, x является целым числом, то анализ можно провести, введя случайную величину S=S(x), такую, что T=K+S, где T является продолжительностью предстоящей жизни, K- пошаговой продолжительностью предстоящей жизни, а S – случайной величиной, представляющей прожитую дробную часть года, в котором наступила смерть. Поскольку K является неотрицательной целочисленной случайной величиной, а – случайной величиной непрерывного типа, вся масса которой сосредоточена на интервале (0,1), мы можем исследовать их совместное распределение, записав
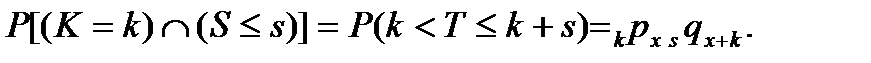
Теперь, воспользовавшись выражением для 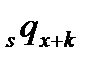 в предположении равномерности распределения, как показано в табл.1, записав
в предположении равномерности распределения, как показано в табл.1, записав
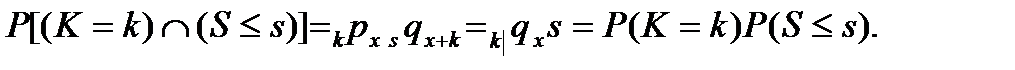
Таким образом, совместное распределение с.в. K и S может быть разложено на произведение маргинальных распределений с.в. K и S. Поэтому в предположении равномерности распределения моментов смерти с.в K и S оказываются независимыми. Поскольку распределение 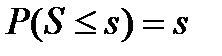 является равномерным на (0,1), с.в. S имеет именно такое равномерное распределение.
является равномерным на (0,1), с.в. S имеет именно такое равномерное распределение.
Равномерное распределение смертей
В этом случае функция выживания интерполируется линейной функцией вида 
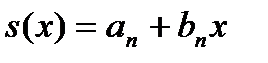 при
при 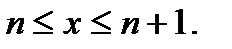 Так как
Так как 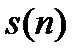 и
и 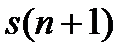 известны (например, из ТПЖ), составляем уравнения:
известны (например, из ТПЖ), составляем уравнения:
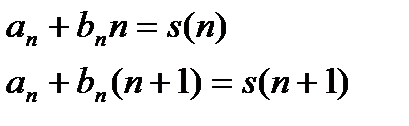
и определяем неизвестные 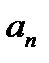 и
и 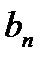 (вычитаем из второго уравнения первое уравнение):
(вычитаем из второго уравнения первое уравнение):
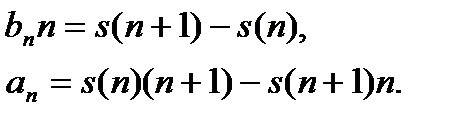
Отметим, что 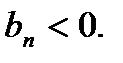
Следовательно, на отрезке 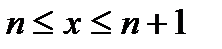 функция
функция 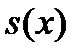 аппроксимируется линейным сплайном вида
аппроксимируется линейным сплайном вида
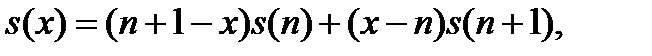
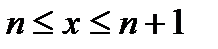 . (2.1.1)
. (2.1.1)
Отсюда для кривой смертей 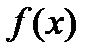 и интенсивности смертности
и интенсивности смертности 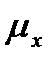 получаем соответственно:
получаем соответственно:
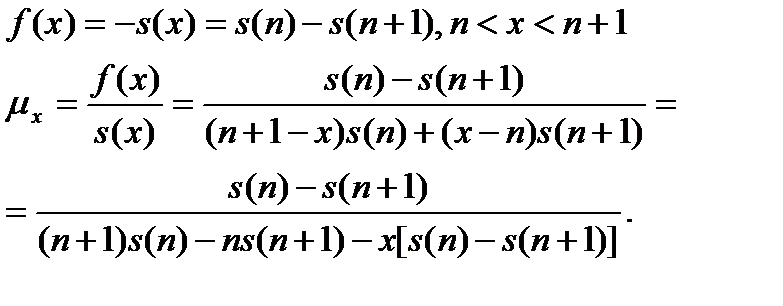 (2.1.2)
(2.1.2)
Таким образом,
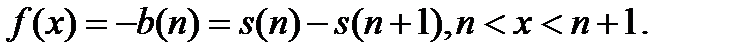
С помощью ранее введенной величины 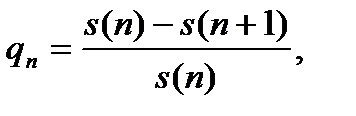 равной вероятности того, что человек в возрасте
равной вероятности того, что человек в возрасте 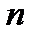 лет умрет в течении ближайшего года, преобразуем формулу (2.1.2) к более удобному виду:
лет умрет в течении ближайшего года, преобразуем формулу (2.1.2) к более удобному виду:
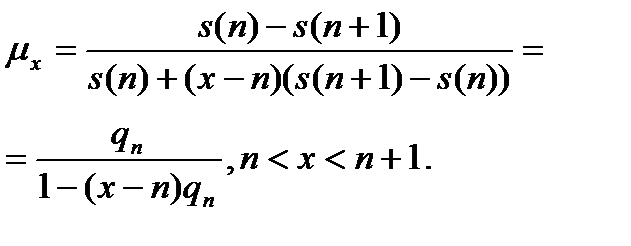
Видим, что приближение влечет возрастание интенсивности смертности
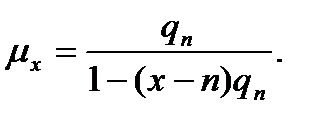 (2.1.3)
(2.1.3)
между узлами интерполяции 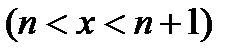 , а плотность распределения
, а плотность распределения 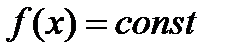 не меняется, причем в целочисленных точках
не меняется, причем в целочисленных точках 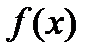 и
и 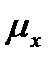 не определены.
не определены.
Заметим, что 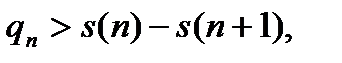 так как
так как 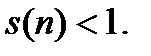
Постоянная интенсивность смертности
Приблизим функцию 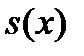 на отрезке
на отрезке 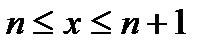 убывающей показательной функции
убывающей показательной функции 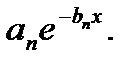 При этом уравнения принимают вид
При этом уравнения принимают вид
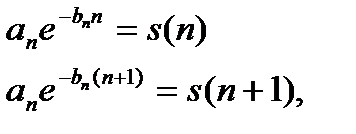
и, разделив второе из них на первое, получаем
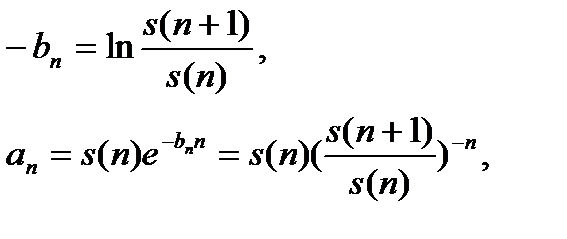
т.е.
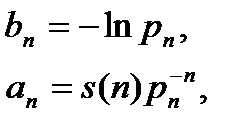
где 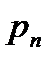 есть вероятность того, что человек в возрасте n лет, проживет, по крайней мере, еще один год.
есть вероятность того, что человек в возрасте n лет, проживет, по крайней мере, еще один год.
В этом случае
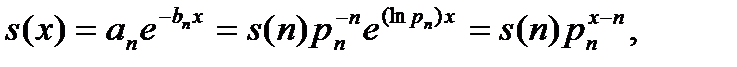
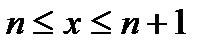
И основные вероятностные характеристики приближенно выражаются следующим образом:
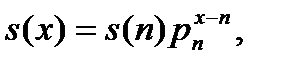
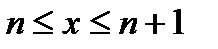
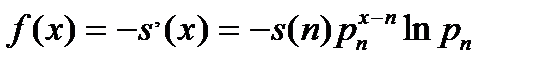 ,
,
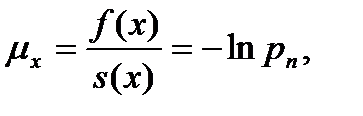
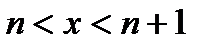 , т.е. между узлами интерполяции
, т.е. между узлами интерполяции 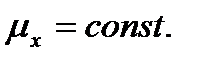
Заметим, что 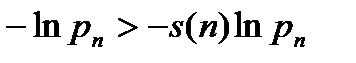 так как
так как 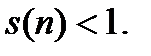
Предположение Балдуччи
В этом случае линейной функцией вместо 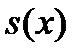 интерполируется
интерполируется 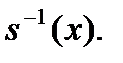
Формально заменяя в (2.1.1) 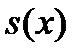 на
на 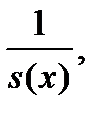 немедленно переходим к соотношению
немедленно переходим к соотношению
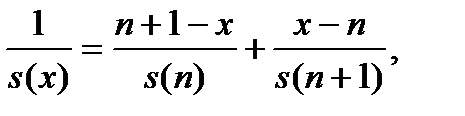
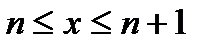 ,
,
Откуда
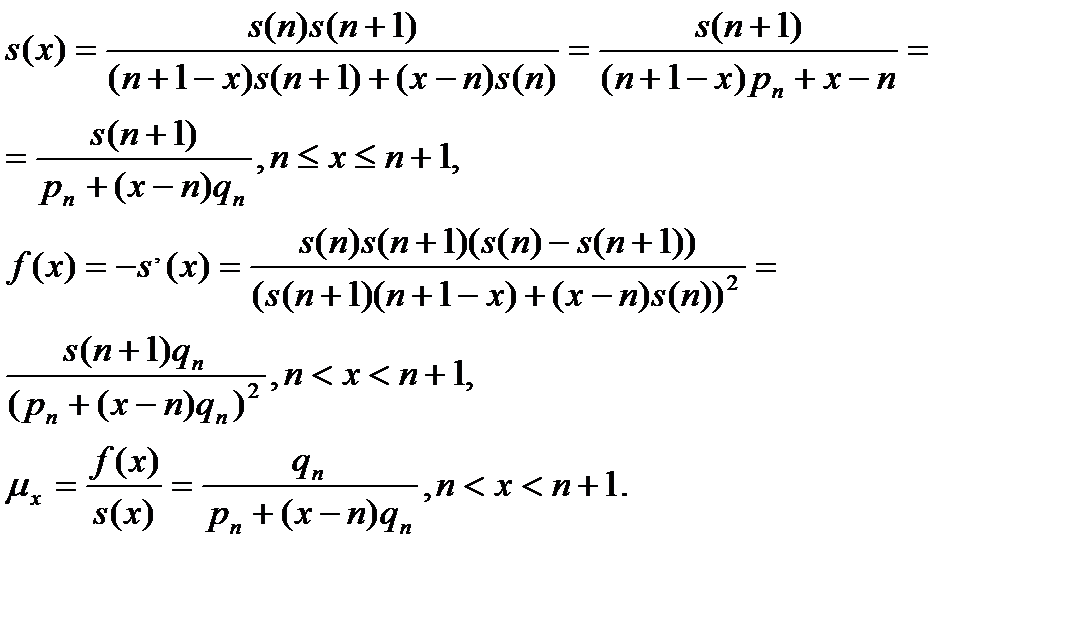
 2015-08-12
2015-08-12 836
836








