Найдем среднее дробного возраста 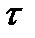 при условии, что смерть наступила в возрасте n лет:
при условии, что смерть наступила в возрасте n лет:
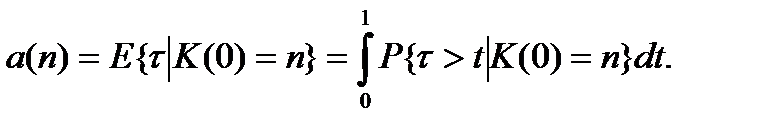
Очевидно, что
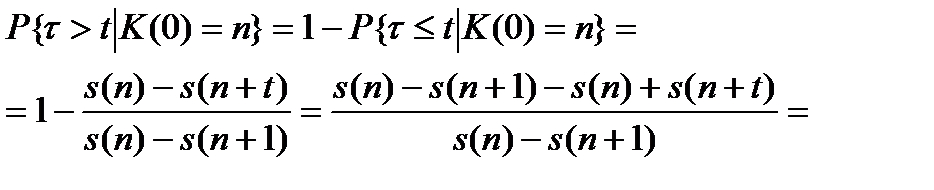
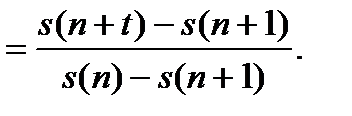
Отсюда
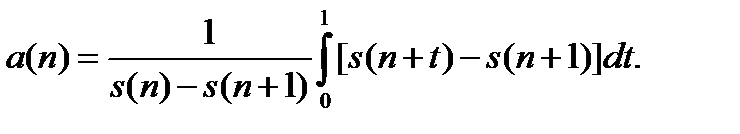
подсчитаем теперь величину 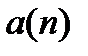 для всех трех предположений о характере смертности для дробных возрастов.
для всех трех предположений о характере смертности для дробных возрастов.
Равномерное распределение смертей
Ясно, что
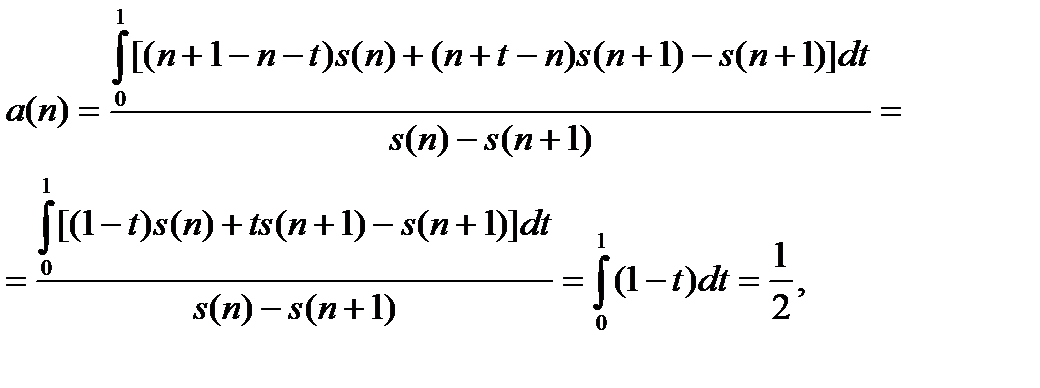
Т.е. 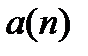 совпадает с серединой одногодичного временного промежутка, то интуитивно мы и ожидали получить.
совпадает с серединой одногодичного временного промежутка, то интуитивно мы и ожидали получить.
Постоянная интенсивность смертности
В этом случае
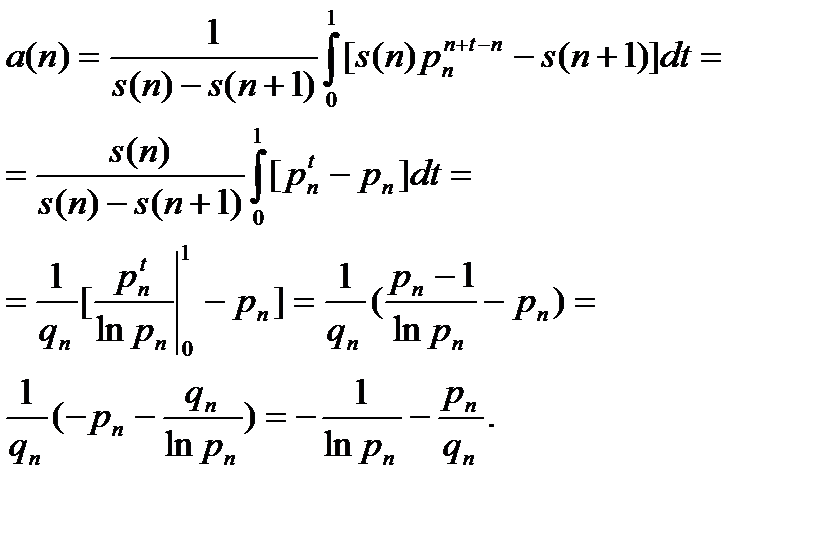
Поскольку 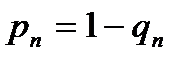 , а
, а 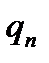 величина достаточно мала, то, воспользовавшись представлением
величина достаточно мала, то, воспользовавшись представлением
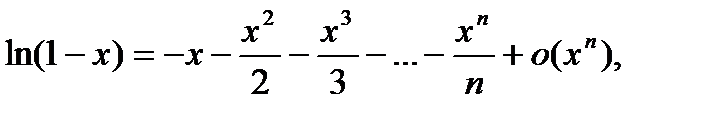
разложим 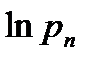 в ряд по степеням
в ряд по степеням 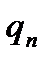
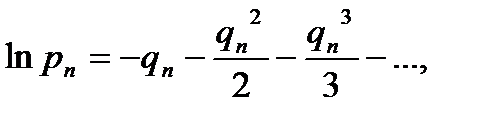
после чего переходим к следующим оценкам для 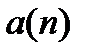 :
:
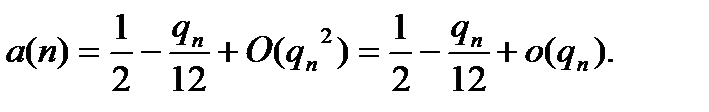 (2.3.1)
(2.3.1)
Докажем равенство (2.3.1). Так как
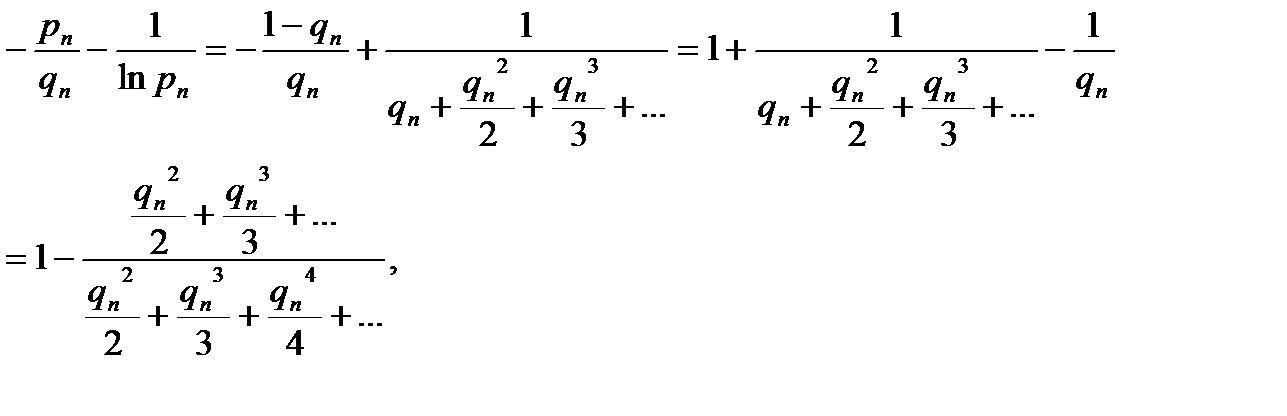
то, разложив функцию (отношение) двух переменных в ряд Тейлора в окрестности точки (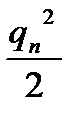 ,
, 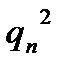 ), получаем
), получаем
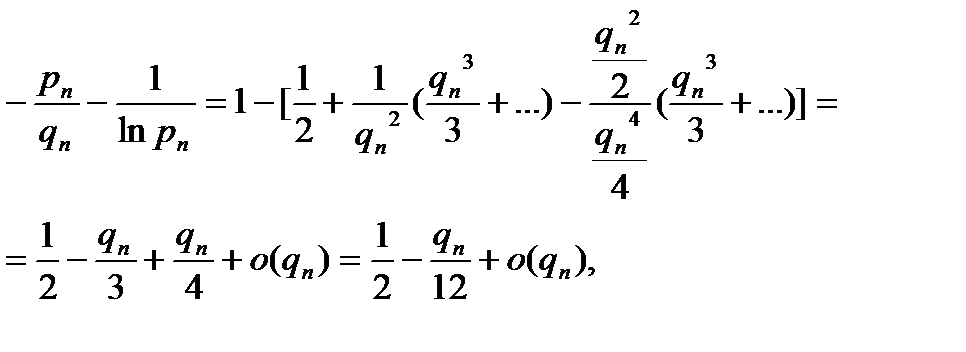
что и требовалось доказать.
Если 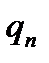 не слишком мало, то имеет смысл учитывать и слагаемые порядка
не слишком мало, то имеет смысл учитывать и слагаемые порядка 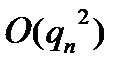 :
:
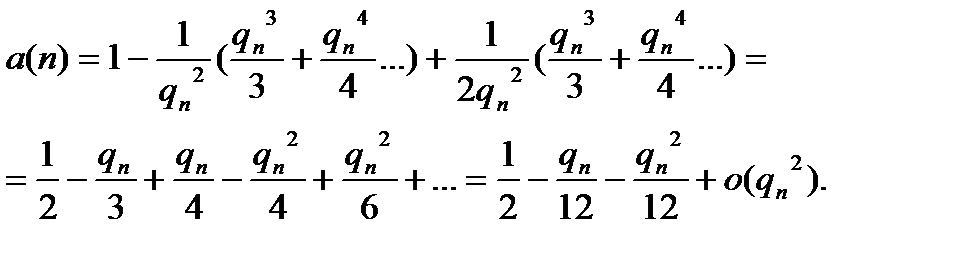
Постулат Балдуччи
Здесь
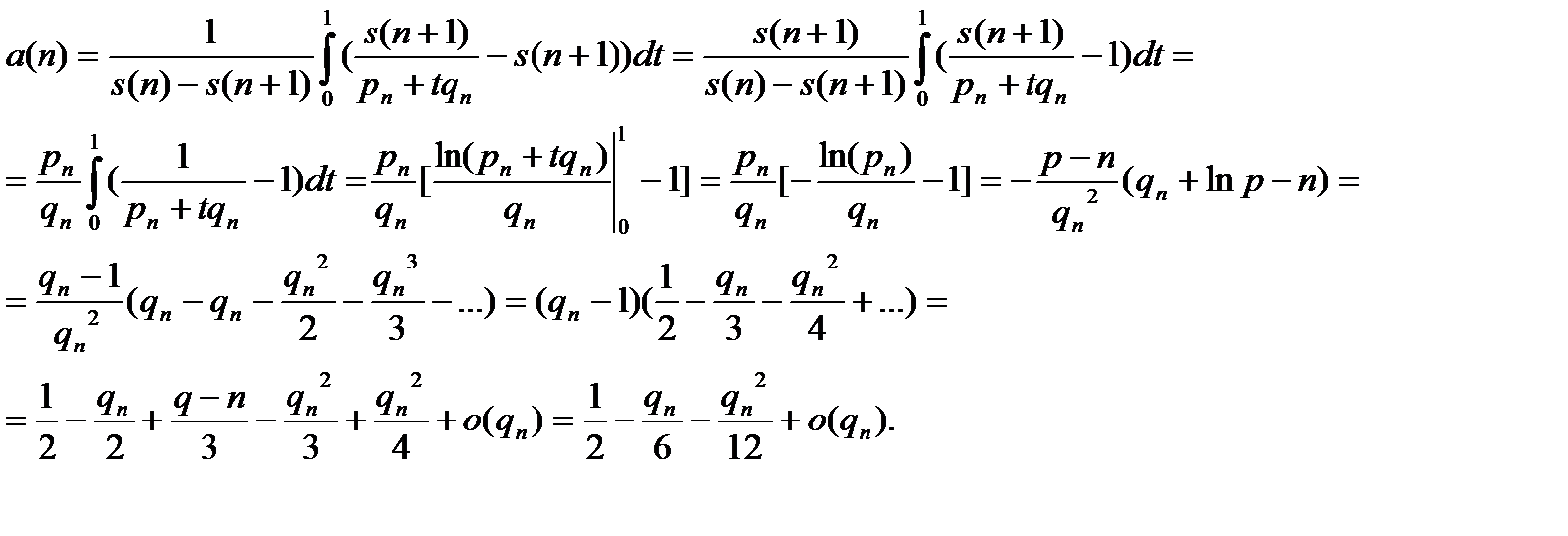
Дисперсию будем находить по следующей формуле:
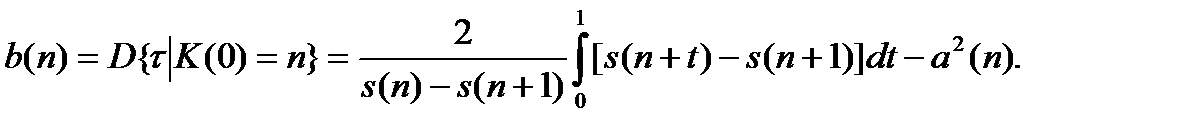
Подсчитаем величину 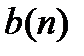 для всех трех постулатов смертности дробных возрастов.
для всех трех постулатов смертности дробных возрастов.
Равномерное распределение смертей
Для этого постулата
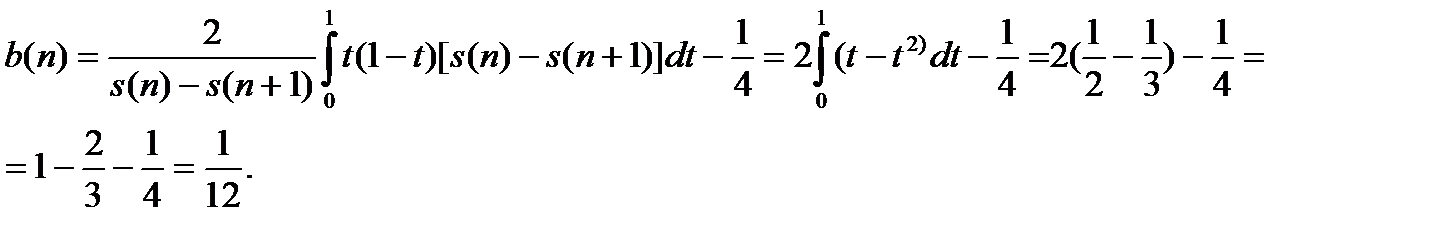
Постоянная интенсивность смертности
Ранее мы получили, что
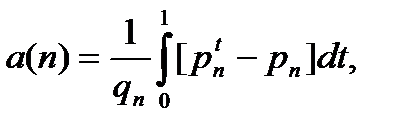
поэтому
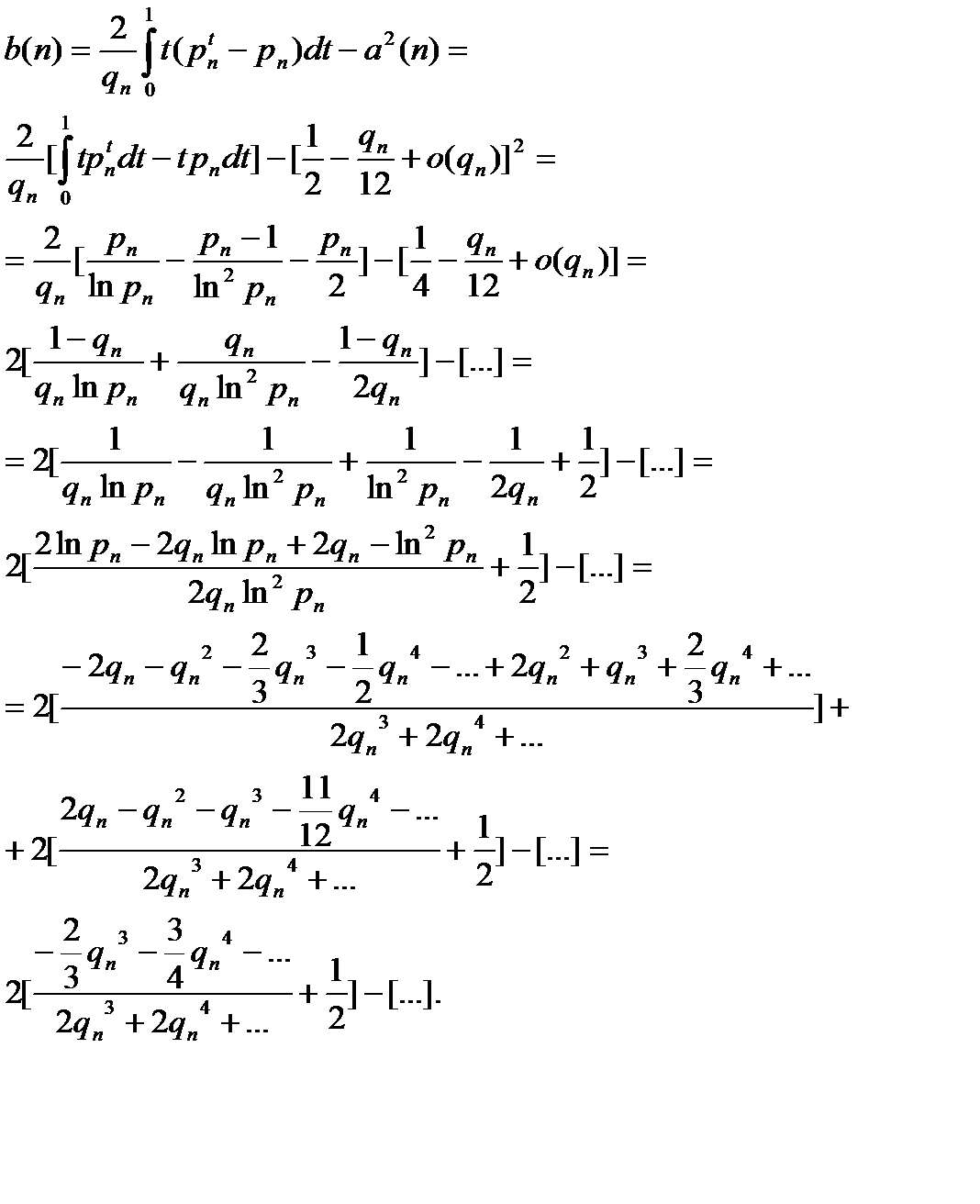
после разложения отношения в ряд Тейлора в окрестности точки
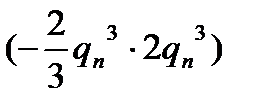 имеем
имеем
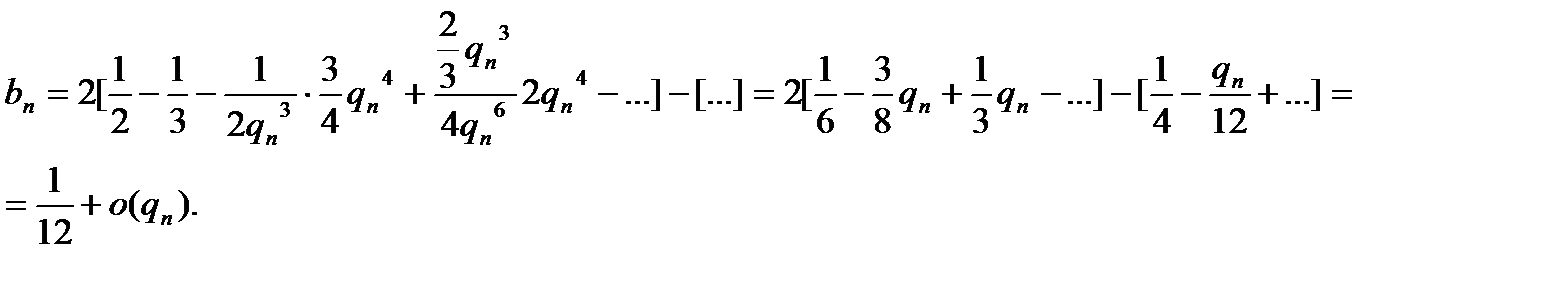
Постулат Балдуччи
Здесь
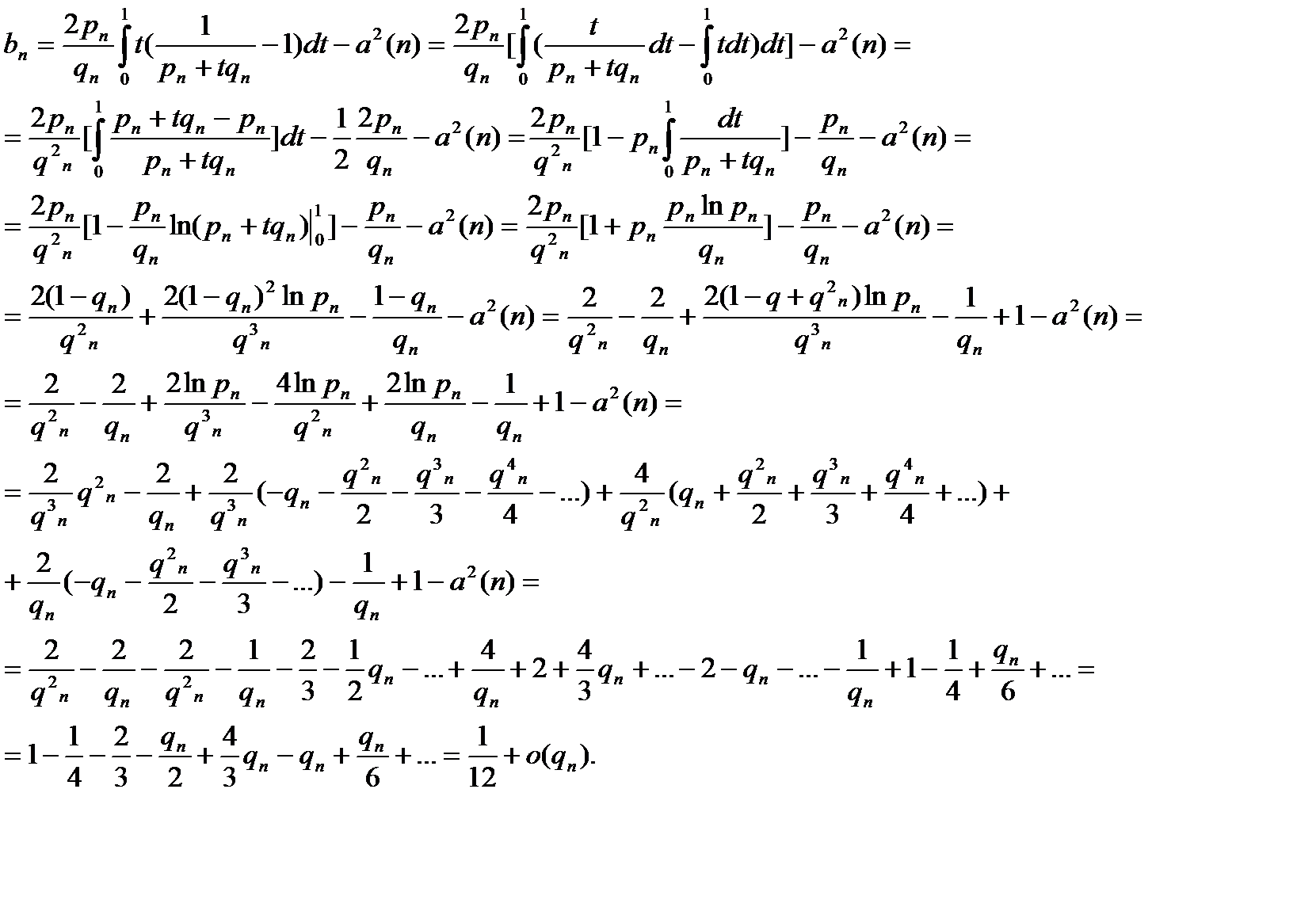
Также на практике в некоторых случаях согласно полученным выше результатам, предположив независимость 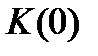 и
и 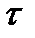 , можно использовать следующие простые аппроксимации для среднего и дисперсии остаточного времени жизни:
, можно использовать следующие простые аппроксимации для среднего и дисперсии остаточного времени жизни:
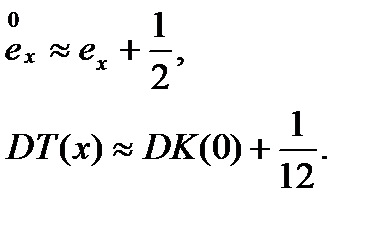
 2015-08-12
2015-08-12 463
463








