Иногда к ним добавляют связь импликации и дизъюнкции

10) A→B = A∨B

3) ф-ии n-переменных Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

4) Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2^{2 n} .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 ⁿ, где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2^m=2^{2 n} .

5) задание ф-й формулами Так же, как составные высказывания строятся из более простых, с помощью логических операций, можно комбинировать булевы переменные с помощью булевых опе­раций, получая булевы выражения, которые называются формулами.

Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию.

6)суперпозиция 7)СДНФ СКНФ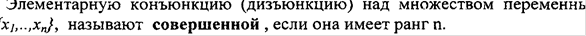

8)представление полиномом жегалкина

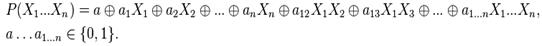
9)методы нахождения полиномов

10) функц полнота

11) полная с-ма операций

В алгебре множеств 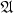для каждого 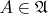определено дополнени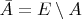е , где 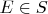- единица алгебры .

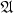Таким образом, в кольце множеств полной системой операций может быть, например, пара операци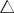й и , а в алгебре множеств нужно ещё добавить нульарную операцию 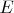(единичный элемент).

12)классы Поста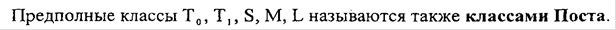

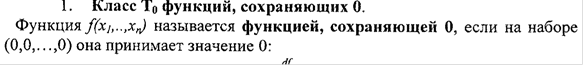
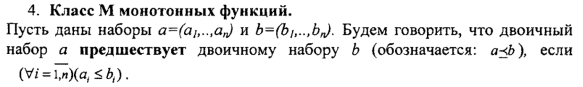
13)замкнутость классов

14)Леммы о функ-ях за…

.

15)критерий полноты

16)предполнота

Графы