
3)соседство
4)степени 

5)способы задания 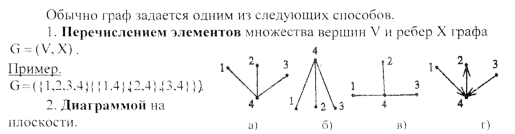


6)виды: Граф называется плоским (планарным), если его можно уложить на плоскости так, чтобы его ребра нигде не пересекались, кроме как в вершинах. Двудольный граф (или биграф, или чётный граф) — это граф G(V,E), такой что множество вершин V разбито на два непересекающихся подмножества V1 и V2, причём всякое ребро E инцидентно вершине из V1 и вершине из V2 (то есть соединяет вершину из V1 с вершиной из V2) Два графа G=(X,U) и L=(X',U') являются изоморфными, если между парами множеств их вершин, ребер и дуг существуют взаимно однозначные соответствия, сохраняющие смежность и ориентацию для дуг 

7)абстрактный и конкретный граф Абстрактный граф - класс изоморфных графов.
8) изоморфизм

9) оценка числа графов 
10)Лемма рукопожатиях и ее следствия 
11) маршруты, цепи. циклы



12)Эйлеровы графы 
13) критерий Эйлеровости 
14 )гамильтоновы 
15)достаточные условия 
16 )планарные и плоские графы 

17) формулы эйлера, гомеоморфные 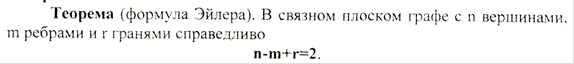



 2015-08-21
2015-08-21 470
470







