Сбор статистических данных для получения оценок характе-ристик случайных величин

Основными элементами, из совокупности которых складываете вероятностная модель метода статистических испытаний, являются случайные реализации. Очевидно, что при решении некоторой задачи деления характеристик или параметров исходного случайного цесса должен быть определен этот случайный процесс.

Искомыми величинами при использовании метода статистиче­ских испытаний являются оценки:

- вероятности наступления некоторого события;

- математического ожидания случайной величины;

- дисперсии случайной величины;

- коэффициентов ковариации или корреляции случайной вели­чины.

Для оценки вероятности р наступления некоторого события А используется частота наступления этого события

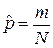(3.01)

где 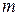- частота наступления события, а 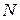- число опытов.

Для оценки математического ожидания случайной величины ис­пользуется среднее значение

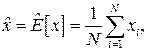(3.11)

где 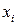- i -я реализация случайной величины.

Для оценки дисперсии случайной величины 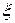, используют фор­мулу

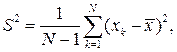(3.12)

где 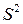- оценка дисперсии случайной величины .

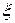Непосредственно использовать эти формулы для вычисления дисперсии сложно, поскольку среднее значение изменяется по мере скопления 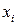, то есть нужно запоминать все N значений 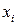. Поэтому для вычисления используют формулу:

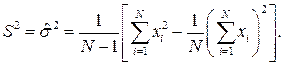(3.13)

В этом случае достаточно накапливать две суммы значени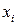й - и .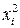

Непосредственное использование этой формулы для программирования может привести к переполнению разрядной сетки, если программировать ее в таком порядке, в котором она записана. Необходимо изменить последовательность действий, чтобы избавиться от очень больших чисел и переполнения разрядной сетки компьютера.

Все статистические оценки должны иметь определенные качественные показатели, к которым относятся несмещенность, эффективность и состоятельность оценки.

Для случайных величин 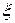и 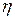с возможными значениями 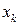, 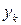оценка корреляционного момента определяется так

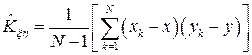(3.14)

или в удобной для вычислений форме

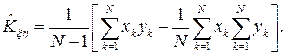(3-15)