Моделирование непрерывных случайных величин

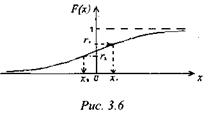
В данном случае используется метод обратной функции. Пусть есть некоторая функция распределения случайной величины (рис. 3.6). Разыграем на оси ординат точку r, используя функ­цию F(x). Тогда можем получить значение величины х такое, что F(x)=r.

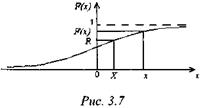
Найдем функцию распределения F(x) случайной величины X. По определению она равна вероятности Р(Х <х). Из рис. 3.7 очевид­но, что

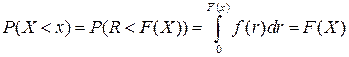(3.4)

Таким образом, последовательность принадлежащая R(0,1), преобразуется в последовательность 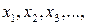которая имет заданную функцию плотности распределения f(x).

Моделирование равномерного распределения в интервал (а, b) случайной величины. Для моделирования воспользуемся методом обратной функции. На рис. 3.8 показана функция плотности равномерного распределения.

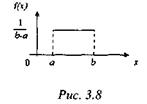
Находим функцию распределения и приравниваем ее к случай­ному числу

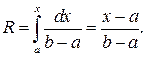(3.5)

Отсюда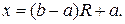

Моделирование экспоненциального распределения случай­ной величины. Функция плотности экспоненциального распределе­ния случайной величины 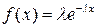и функция распределения пока­заны на рис. 1.1.

Воспользуемся методом обратной функции:

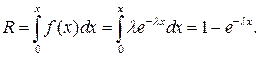(3.6)

Из выражения (3.6) находим х:

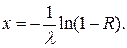(3.7)

Можно показать, что случайная величина (1-R) распределена так же, как и величина R. Тогда, сделав замену (1-R) на R, получаем

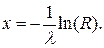(3.3.5)

Покажем, как, используя метод обратной функции, можно моделировать случайную величину, распределенную по экспоненциаль­ному закону. Подобный подход принят в языке GPSS [10].

Пусть 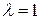. Выполним аппроксимацию функции экспоненци­ального распределения линейными участками, чтобы можно был использовать ее для моделирования методом обратной функции. Для аппроксимации достаточно 24 точек. В табл. 3.2 занесены соответствующие значения аргумента х и функции F(x), значения которой генерируют с помощью генератора случайных чисел.

Таблица 3.2

x	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.75	0.8	0.84	0.88
F(x)	0	0.1	0.222	0.355	0.509	0.69	0.915	1.2	1.38	1.6	1.83	2.12

x	2.3	2.52	2.81	2.99	3.2	3.5	3.9	4.6	5.3	6.2	7	8
F(x)	0.9	0.92	0.94	0.95	0.96	0.97	0.98	0.99	0.995	0.998	0.999	0.9998

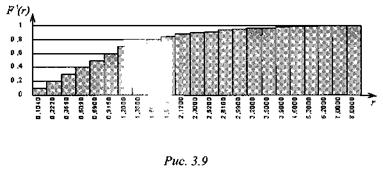
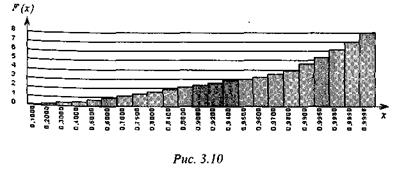
На рис. 3.9 и 3.10 показаны графики двух функций. На рис. 3.9 изображена аппроксимация экспоненциальной функции с параметром 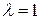, а на рис. 3.10 - функция, обратная к аппроксимированной. Пер­вая функция воспроизводит заданные в табл. 3.2 значения. Вторая функция используется для розыгрыша экспоненциального распреде­ления, поскольку удобнее задавать значение х, а получать значение функции. Если необходимо моделировать случайные величины X, распре­деленные по экспоненциальному закону с параметром 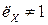, кото­рые используется как задержка во времени с параметром 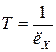, например, для моделирования пуассоновского потока поступления тре­бований, то поступают таким образом:

- генерируют значения случайной величины, распределенной по экспоненциальному закону с (рис. 3.10);

- находят произведение полученного значения и математиче­ского ожидания случайной величины .

В результате получают искомую последовательность значений реализации случайной величины X.

Моделирование нормального закона распределения слу­чайной величины. Для моделирования нормального закона распре­деления случайной величины нельзя непосредственно воспользовать­ся методом обратной функции, поэтому используем центральную предельную теорему. Пусть случайная величина X имеет математиче­ское ожидание 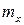и среднеквадратичное отклонение 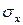, а случайная величина Z имеет математическое ожидание 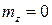и среднеквадра­тичное отклонение 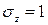. Легко показать, что

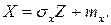(3.8)

Сформулируем центральную предельную теорему.

Если 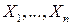- независимые случайные величины со средним значением 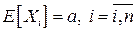и дисперсией 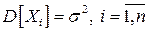, то при неограниченном увеличении n функция распределения случайной величины 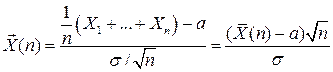приближается к функции распределения стандартного нормального закона 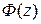при всех значениях аргумента, то есть

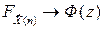(3.9)

где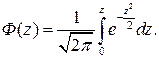

Для получения нормального закона распределения случайной величины достаточно суммировать шесть случайных величин, полученных с помощью генератора случайных чисел R, и, пронормировав лученные значения так, чтобы определить Z, по формуле (3.8) най­ти значение X.

Обычно суммируют 12 случайных величин 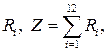тогда дисперсия D(Z) будет равняться единице.

Рассмотрим, как моделируются нормально распределенные слу­чайные величины в системе моделирования GPSS.

Выполним аппроксимацию функции нормального распределе­ния случайной величины Z с параметрам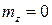и и 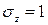. Для этого достаточно 25 точек. В табл. 3.3 занесенные соответствующие значе­ния аргумента х и функции F (х).

Для того, чтобы получить функцию нормального распределения с математическим ожиданием 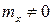и среднеквадратичным отклоне­нием , необходимо сделать вычисления по формуле (3.8).

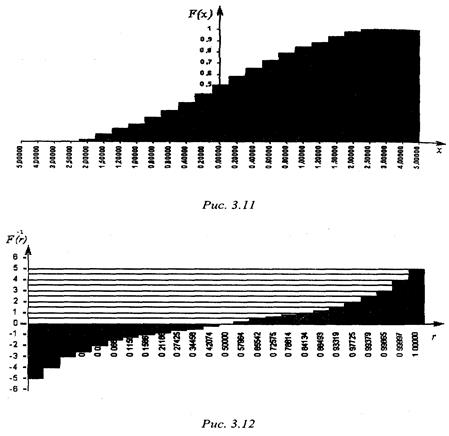
На рис. 3.11 изображен график функции, полученной в резуль­тате аппроксимации функции нормального распределения , а на рис. 3.12 - более удобный для моделирования график функции (как аргумент используют генератор случайных чисел и получают значе­ние функции).

Таблица 3.3

x	-5	4	3	-2.5	-2	-1.5
F(x)	0	0.00003	0.00135	0.00621	0.02275	0.06681

x	-1.2	-1	-0.8	-0.6	-0.4	-0.2
F(x)	0.11507	0.15866	0.21186	0.27425	0.34458	0.42704

x	0	0.2	0.4	0.6	0.8	1
F(x)	0.5	0.57964	0.65542	0.72575	0.78814	0.84134

x	1.2	1.5	2	2.25	3	4	5
F(x)	0.88493	0.93319	0.97725	10.99379	0.99865	0.999971	1

Если необходимо обеспечить положительные разыгрываемые значения, то нужно выполнить условие .

В рассмотренных приближенных методах «хвосты» нормально­го распределения оказываются неточными. Существуют и более точные методы моделирования нормального распределения случаи' ной величины [11].