Пусть среднее значение интервалов поступления Т в пуассоновском потоке требований равно 2 ч, а единица времени в модели равна 1 мин, тогда поступление заявок моделируется блоком:
GENERATE 120,FN$XPDIS
Если необходимо моделировать задержку, распределенную по экспоненциальному закону со средним значением времени 345, то для этого используется блок:
ADVANCE 345,FN$XPDIS
 Свойство ординарности пуассоновского потока гласит: вероятность поступления двух или более заявок в течение малого временного интервала равна нулю.
Свойство ординарности пуассоновского потока гласит: вероятность поступления двух или более заявок в течение малого временного интервала равна нулю.
Пусть пуассоновский поток моделируется блоком
GENERATE 5,FN$XPDIS
Если в результате обращения к функции XPDIS полученное значение меньше, чем 1/5, то целая часть произведения числа 5 и значения функции XPDIS равна нулю. Отсюда следует нарушение свойства ординарности. Во избежание этого рекомендуется, чтобы операнд А в блоке GENERATE был больше 50. Это легко достигается путем варьирования значения единицы модельного времени.
Моделирование гипер- и гипоэкспоненциального распределений.
Экспоненциальную функцию распределения можно использовать также для моделирования гипер- и гипоэкспоненциального распределений.
Неэкспоненциальное распределение с коэффициентом вариации { Коэффициент вариации С - это отношение стандартного отклонения к математическому ожиданию случайной величины.} С > 1 можно получить с помощью взвешенной суммы экспонент - гиперэкспоненциального распределения:
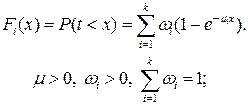 (4.3)
(4.3)
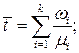 (4.4)
(4.4)
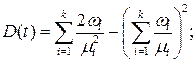 (4.5)
(4.5)
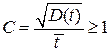 (4.6)
(4.6)
Если 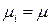 для всех i, то С = 1 — имеем экспоненциальное распределение.
для всех i, то С = 1 — имеем экспоненциальное распределение.
Гиперэкспоненциальное распределение можно получить при параллельном соединении k (рис. 4.6) экспоненциальных обслуживающих устройств с интенсивностью обслуживания 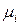 и вероятностью
и вероятностью 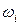 , использования для обслуживания (
, использования для обслуживания (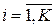 ). Причем в произвольный момент времени может быть занято не более одного устройства из k.
). Причем в произвольный момент времени может быть занято не более одного устройства из k.
Такое распределение хорошо описывает распределение времени работы центрального процессора компьютера.
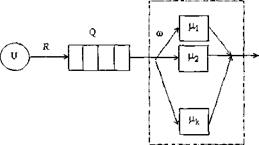
Рис. 4.6
Для моделирования гиперэкспоненциального распределения со средним значением 6,28 и стандартным отклонением 8,4 необходимо определить переменную
HYP FVARIABLE (410+(RN2 'L1 234)(#(1334 -410)))#FN$XPDIS
Эту переменную можно использовать в блоке задержки так:
ADVANCE V$HYP
Гипоэкспоненциольное распределение с коэффициентом вариации С <1 описывается таким образом:
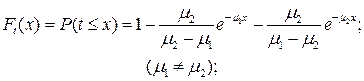 (4.7)
(4.7)
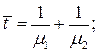 (4.8)
(4.8)
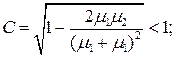 (4.9)
(4.9)
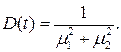 (4.10)
(4.10)
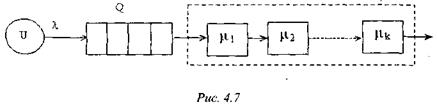
При равенстве всех коэффициентов 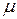 распределение времени пребывания в обслуживающем центре (на рис. 4.7 обведен пунктирной линией) будет k-распределением Эрланга:
распределение времени пребывания в обслуживающем центре (на рис. 4.7 обведен пунктирной линией) будет k-распределением Эрланга:
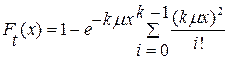 (4.11)
(4.11)
Гипоэкспоненциальное распределение характерно, например, для времени обслуживания устройств ввода-вывода. Его можно получить последовательным соединением обслуживающих экспоненциальных устройств, причем в любой момент времени должно быть занято не более одного устройства (рис. 4.7).
Моделирование эрланговского потока. Экспоненциальное Распределение не всегда адекватно описывает время обслуживания и поступления требований в систему. Более реалистичным является Распределение Эрланга. В то же время, это распределение является Частньщ случаем гамма-распределения, которое описано ниже. Для пoтока Эрланга k -го порядка с интенсивностью 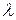 математическое ожидание и дисперсия определяются так:
математическое ожидание и дисперсия определяются так: 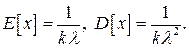 . Для моделирования распределения Эрланга может также использоваться экспоненциальная функция распределения. Как было показано в главе 1, для этого достаточно просуммировать k случайных экспоненциально распределенных величин. С ростом k распределение Эрланга будет приближаться к нормальному распределению. Например, поток Эрланга второго порядка со средним значением времени поступления 180 можно задать таким образом:
. Для моделирования распределения Эрланга может также использоваться экспоненциальная функция распределения. Как было показано в главе 1, для этого достаточно просуммировать k случайных экспоненциально распределенных величин. С ростом k распределение Эрланга будет приближаться к нормальному распределению. Например, поток Эрланга второго порядка со средним значением времени поступления 180 можно задать таким образом:
GENERATE,„1
SDFG ADVANCE 90,FN$EXPDIS
ADVANCE 90,FN$EXPDIS
 2015-08-21
2015-08-21 660
660








