Lognormal(stream, Locate, Scale, shape)

где Stream — номер генератора случайных чисел, автоматически пре­образуется в целое число, которое должно быть больше или равно 1; Locate = 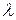; Scale = 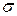; Shape = 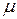. Все параметры обязательные.

Гамма-распределение является обобщенным распределением Эрланга для случая, когда число 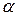суммируемых величин является нецелым. Гамма-распределенная величина имеет значения от 0 до 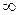, то есть неотрицательна. Если 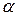- целое, то это будет распределение Эрланга.

Функция распределения значительно изменяет свою форму при различных параметрах, что позволяет использовать это распределе­ние для моделирования различных физических явлений.

Гамма-распределение можно интерпретировать как сумму квад­ратов нормально распределенных случайных величин, то есть как 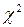-распределение.

Таким образом, 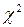-распределение, распределение Эрланга и экспоненциальное распределение являются частными случаями гам­ма-распределения.

Функция плотности гамма-распределения имеет вид:

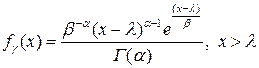(4.16)

где 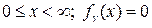если x <0; 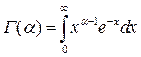- гамма функция Эйлера.

Математическое ожидание и дисперсия гамма-распределенной случайной величины таковы:

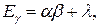(4.17)

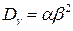(4.19)

где параметр 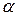задает форму распределения, 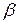- масштаб для сжатия или растяжения распределения, 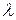- величину сдвига для определения местоположения распределения.

Для вызова гамма-распределения используется библиотечная процедура