2015-08-21
1266
Пусть целевая функция f(x) ограничена снизу и непрерывно дифференцируема в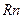 
. Предположим, что существует точка 
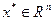,в которой эта функция достигает локального минимума. Рассмотрим некоторые особенности применения метода градиентного спуска для поиска этой точки.
В этом методе элементы релаксационной последовательности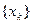 
удовлетворяют рекуррентному соотношению вида 
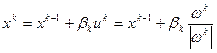. Тут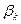 
- шаг спуска, а направление спуска задано единичным вектором 
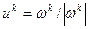, сонаправленным антиградиенту, т.е. 
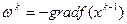. Пусть 
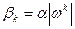, где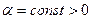 
-шаг спуска на каждой итерации пропорционален длине вектора антиградиента в точке 
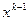. Если функция f(x) непрерывно дифференцируема в 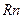, то скалярное произведение
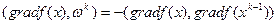является непрерывной функцией. Ясно, что функция f(x) убывает в
направлении антиградиента до тех пор, пока это произведение остается отрицательным. Поэтому один из способов выбора значения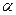 
на к-й итерации состоит в том, чтобы 
.
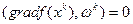Указанный способ называют исчерпывающим спуском
