Методы спуска. Оценка спуска для выпуклых дифференцируемых в Rn функциях

Пусть существует точка 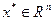, в которой целевая функция f(x) достигает минимума. Процедуру поиска этой точки в методах спуска обычно описывают (после выбора начальной точки х0) рекуррентным соотношением 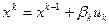. (А). где 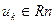— единичный вектор, определяющий направление спуска на к итерации, а 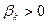— длина шага спуска, т.е. расстояние в этом направлении, отделяющее точку 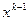от новой точки 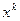. Методы спуска различаются способами выбора направления и шага спуска.

<!--

Если на к-й итерации выбран вектор 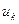, то один из способов выбора значения 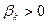базируется на требовании, чтобы выполнялось неравенство: 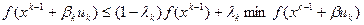(В), где 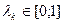. Отметим, что выбор значения 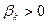в соответствии с последним неравенством обеспечивает что последовательность 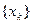, построенная в соответствии (А), будет релаксационной.

При 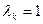неравенство (В) переходит в равенство, а значение 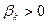соответствует минимальному значению f(x) на множестве 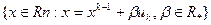. В этом случае для нахождения 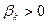надо решить задачу одномерной оптимизации.

-->

Лемма. Если все элементы последовательности 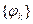подпадают под условие 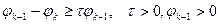то в этом случае справедлива оценк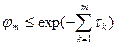а (А).

Теорема. Если ф-я 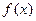выпукла и дифференцируема в некотором множестве 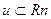, а 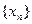-релаксационная последовательность, то при

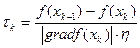, где 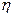- диаметр множества 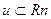, выполняется оценка (А) ил вышеприведенной леммы.

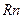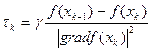Теорема. Для сильно выпуклой функции дифференцируемой в при , где 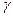-параметр сильной выпуклости, 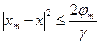. Последнее неравенство задает сходимость по точкам релаксационной последовательности.