Релаксационная последовательность, Оценка сходимости для выпуклых дифференцируемых функций

Релаксационная последовательность, Оценка сходимости.

Последовательность точек 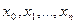называется релаксационной, если для каждой точки 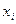выполняется .

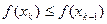Введем 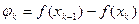. Последовательность 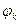- сходящаяся, и 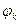=0 тогда когда 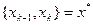. Последовательность 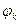положительная, но при переходе через х^* - отрицательная.

Релаксационная последовательность, Оценка сходимости для выпуклых дифференцируемых функций.

Теорема. Пусть минимизируемая ф-я 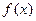выпукла и дифференцируема на 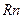, и последовательность 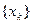есть релаксационной. Тогда, если 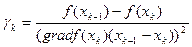, то справедлива следующая лемма:

Лемма

Если для элементов последовательности 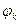справедливо 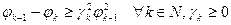, то справедлива оценка вид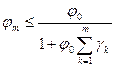а:

. (А)

Доказательств о: Разделим 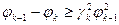на 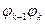. Получим:

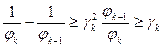. Просуммировав это, получим: 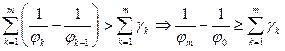. Решая последнее неравенство и получим нашу оценку (А)