Метод подразумевает последовательное нахождение экстремума функции цели по каждой из координат.
Пусть имеем 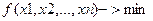 . Производится последовательная минимизация функции по каждой из координат. Пусть
. Производится последовательная минимизация функции по каждой из координат. Пусть 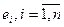 , — стандартный базис в
, — стандартный базис в 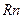 . Выберем начальную точку х0. Поиск точки минимума функции в методе циклического покоординатного спуска проводят в соответствии с рекуррентным соотношением
. Выберем начальную точку х0. Поиск точки минимума функции в методе циклического покоординатного спуска проводят в соответствии с рекуррентным соотношением 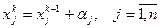 . Значение
. Значение 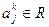 находят из решения задачи одномерной минимизации
находят из решения задачи одномерной минимизации 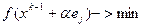 . Подчеркнем, что индекс j изменяется циклически, пробегая на каждом шаге покоординатного спуска все значения от 1 до
. Подчеркнем, что индекс j изменяется циклически, пробегая на каждом шаге покоординатного спуска все значения от 1 до 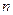 , причем значение
, причем значение 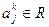 может быть как положительным, так и отрицательным. Для каждого значения
может быть как положительным, так и отрицательным. Для каждого значения 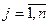 из решения задачи одномерной минимизации находят значение
из решения задачи одномерной минимизации находят значение 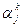 и затем вычисляют
и затем вычисляют 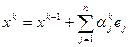 , и
, и 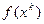 . Далее проверяют выполнение одного (или обеих) условий:
. Далее проверяют выполнение одного (или обеих) условий: 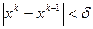 - сильное условие сходимости.
- сильное условие сходимости. 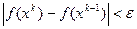 - слабое условие сходимости. В случае их выполнение полагают
- слабое условие сходимости. В случае их выполнение полагают 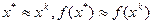 .
.
 2015-08-21
2015-08-21 432
432








