2015-08-21
436
Методы, используемые при обучении нейронных сетей, во многом аналогичны методам определения экстремума функции нескольких переменных. В свою очередь, последние делятся на 3 категории – методы нулевого, первого и второго порядка.
В методах нулевого порядка для нахождения экстремума используется только информация о значениях функции в заданных точках.
В методах первого порядка используется градиент функционала ошибки по настраиваемым параметрам
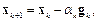(3.16)
где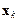 
– вектор параметров; 
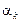– параметр скорости обучения; 
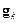– градиент функционала, соответствующие итерации с номером k.
Вектор в направлении, противоположном градиенту, указывает направление кратчайшего спуска по поверхности функционала ошибки. Если реализуется движение в этом направлении, то ошибка будет уменьшаться. Последовательность таких шагов в конце концов приведет к значениям настраиваемых параметров, обеспечивающим минимум функционала. Определенную трудность здесь вызывает выбор параметра скорости обучения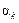 
. При большом значении параметра 
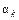сходимость будет быстрой, но существует опасность пропустить решение или уйти в неправильном направлении. Классическим примером является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, перепрыгивая с одного на другой. Напротив, при малом шаге, вероятно, будет выбрано верное направление, однако при этом потребуется очень много итераций. В зависимости от принятого алгоритма параметр скорости обучения может быть постоянным или переменным. Правильный выбор этого параметра зависит от конкретной задачи и обычно осуществляется опытным путем; в случае переменного параметра его значение уменьшается по мере приближения к минимуму функционала.
В алгоритмах сопряженного градиента [12] поиск минимума выполняется вдоль
сопряженных направлений, что обеспечивает обычно более быструю сходимость, чем
при наискорейшем спуске. Все алгоритмы сопряженных градиентов на первой итерации начинают движение в направлении антиградиента
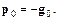(3.17)
Тогда направление следующего движения определяется так, чтобы оно было сопряжено
с предыдущим. Соответствующее выражение для нового направления движения является комбинацией нового направления наискорейшего спуска и предыдущего направления:
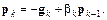(3.18)
Здесь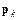 
– направление движения, 
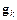– градиент функционала ошибки, 
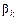– коэффициент соответствуют итерации с номером k. Когда направление спуска определено,
то новое значение вектора настраиваемых параметров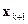 
вычисляется по формуле
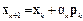. (3.19)
Методы второго порядка требуют знания вторых производных функционала ошибки.
К методам второго порядка относится метод Ньютона. Основной шаг метода Ньютона определяется по формуле
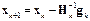, (3.20)
где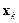 
– вектор значений параметров на k- й итерации; H – матрица вторых частных производных целевой функции, или матрица Гессе; 
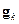– вектор градиента на k- й итерации. Во многих случаях метод Ньютона сходится быстрее, чем методы сопряженного градиента, но требует больших затрат из-за вычисления гессиана. Для того чтобы избежать вычисления матрицы Гессе, предлагаются различные способы ее замены приближенными выражениями, что порождает так называемые квазиньютоновы алгоритмы (алгоритм метода секущих плоскостей OSS [1], алгоритм LM Левенберга – Марквардта [17]).
