Создание сети

В ППП NNT для создания LVQ-сетей предусмотрена М-функция newlvq, обращение
к которой имеет следующий вид:

net = newlvq(PR,S1,PC,LR,LF)

где PR – массив размера R´2 минимальных и максимальных значений для R элементов вектора входа; S1 – количество нейронов конкурирующего слоя; PC – вектор с S ² элементами, определяющими процентную долю принадлежности входных векторов к определенному классу; LR – параметр скорости настройки (по умолчанию 0.01); LF – имя функции настройки (по умолчанию для версии MATLAB 5 – 'learnlv2', для версии MATLAB 6 – 'learnlv1').

Предположим, что задано 10 векторов входа и необходимо создать сеть, которая,
во-первых, группирует эти векторы в 4 кластера, а во-вторых, соотносит эти кластеры
с одним из двух выходных классов. Для этого следует использовать LVQ-сеть, первый конкурирующий слой которой имеет 4 нейрона по числу кластеров, а второй линейный слой – 2 нейрона по числу классов.

Зададим обучающую последовательность в следующем виде:

P = [–3 –2 –2 0 0 0 0 2 2 3;

0 1 –1 2 1 –1 –2 1 –1 0];

Tc = [1 1 1 2 2 2 2 1 1 1];

Из структуры обучающей последовательности следует, что 3 первых и 3 последних ее вектора относятся к классу 1, а 4 промежуточных – к классу 2. На рис. 7.18 показано расположение векторов входа.

I1 = find(Tc==1); I2 = find(Tc==2);

axis([–4,4,–3,3]), hold on

plot(P(1,I1),P(2,I1),’+k’)

plot(P(1,I2),P(2,I2),’xb’) % Рис.7.18

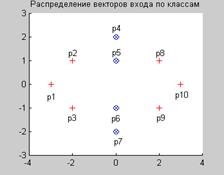Рис. 7.18

Векторы, относящиеся к разным классам, отмечены разными символами. Как следует из расположения векторов, классы не являются линейно отделимыми, и задача не может быть решена с использованием, например, персептрона.

Преобразуем вектор индексов Tc в массив целевых векторов:

T = full(ind2vec(Tc))

T =

1 1 1 0 0 0 0 1 1 1

0 0 0 1 1 1 1 0 0 0

Процентные доли входных векторов в каждом классе равны 0.6 и 0.4 соответственно. Теперь подготовлены все данные, необходимые для вызова функции newlvq. Вызов может быть реализован c использованием следующего оператора

net = newlvq(minmax(P),4,[.6.4],0.1);