Собственные векторы и собственные значения линейных операторов в конечномерном пространстве

Определение 12.1. Пусть A – линейный оператор, действующий из R ⁿ в R ⁿ. Всякий ненулевой вектор x Î R ⁿ называется собственным вектором оператора A (матрицы А), если оператор A переводит вектор x в коллинеарный ему вектор:

Ax = l x. (12.1)

Число l при этом называется собственным значением оператора A (матрицы А), соответствующим собственному вектору x.

Отметим, что если оператор A невырожден, то все его собственные значения отличны от нуля.

В самом деле, если некоторое собственное значение l = 0, то из условия (12.1) получим Ax = 0× x = 0, откуда в силу невырожденности оператора A следует, что собственный его вектор x = 0. Это противоречит определению собственного вектора. Значит, l ¹ 0.

Укажем некоторые свойства собственных векторов.

Пусть для оператора A существует обратный оператор A ^–1. Умножая равенство (12.1) слева на A ^–1, получаем

A ^–1(Ax) = A ^–1(l x) Û x = l A ^–1 x Û A ^–1 x = l ^–1 x,

т. е. l ^–1 является собственным значением оператора A ^–1, соответствующим тому же собственному вектору x.

Из равенства (12.1) получим A (Ax) = A (l x) = l Ax = l ² x, или A ² x = l ² x, т. е. l ² – собственное значение оператора A ², соответствующее тому же собственному вектору x. Аналогично доказывается, что A ^k x = l^k x, где k Î N.

Определение 12.2. Множество всех собственных значений линейного оператора называется его спектром.

Следующие свойства собственных векторов сформулируем в виде теоремы.

Теоремa 12.1. Собственные векторы линейного оператора A, соответствующие попарно различным собственным значениям, линейно независимы.

Доказательство. Теорему докажем индукцией по числу k. Пусть x ¹, x ²,… …, x ^k – собственные векторы, а l ₁, l ₂,…, l_k – соответствующие им попарно различные собственные значения линейного оператора A.

Очевидно, при k = 1 теорема верна. Допустим, что теорема верна для всяких k – 1 собственных векторов оператора A, и покажем, что она останется верной и для любых k собственных векторов.

Предположим противное, т. е. допустим, что k собственных векторов ли-нейно зависимы. Следовательно, справедливо равенство

x ¹ + x ² +…+ 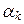x ^k = 0,

где, например, ¹ 0. Подействуем оператором A на векторы, стоящие в обеих частях этого равенства, и получим

l ₁ x ¹ + l ₂ x ² +…+ 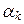l_k x ^k = 0.

Умножая первое равенство на l_k и вычитая его из второго, находим

(l ₁ – l_k) x ¹ + (l ₂ – l_k) x ² +…+ 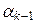(l_{k –1} – l_k) x ^{k –1} = 0,

откуда по предположению индукции все коэффициенты должны быть равны нулю, в том числе и (l ₁ – l_k), что противоречит условиям ¹ 0 и l ₁ ¹ l_k. Значит, наше предположение неверно и векторы x ¹, x ²,…, x ^k линейно независимы.¨

Следствие. В пространстве R ⁿ линейный оператор A не может иметь более n собственных векторов, соответствующих различным собственным значениям (т. к. в R ⁿ всякие n + 1 векторов линейно зависимы).

Теоремa 12.2. Все собственные векторы линейного оператора A, отвечающие одному собственному значению l, вместе с нулевым вектором образуют подпространство данного линейного пространства.

Доказательство. В самом деле, если Ax ¹ = l x ¹ и Ax ² = l x ², то

A ( x ¹ + x ²) = Ax ¹ + Ax ² = l x ¹ + l x ² = l ( x ¹ + x ²), ,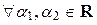

что и доказывает теорему.¨

Таким образом, если x – собственный вектор оператора A, соответствующий собственному значению l, то и всякий вектор 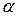x, где 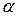¹ 0, тоже является собственным вектором этого оператора, соответствующим собственному значению l. Число a всегда можно вы брать таким, что || 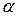x || = 1, т. е. = .

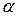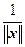Определение 12.3. Собственный вектор, норма которого равна 1, называется нормированным.