Рассмотрим, как найти координаты собственных векторов оператора A, заданного своей матрицей А в некотором базисе е l, е 2,..., е n пространства R n.
Пусть вектор x = (x 1, x 2,…, xn) является собственным вектором оператора A, соответствующим собственному значению l. Тогда соотношение (12.1) в матричной форме перепишется в виде
(А – lЕ) x = 0,
где Е – единичная матрица. Если
А 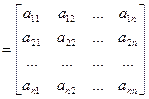 –
–
матрица оператора A, то последнее равенство соответствует однородной системе n уравнений
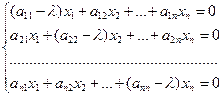 (12.2)
(12.2)
относительно n неизвестных x 1, x 2,…, xn – координат собственного вектора x. Нас интересуют только нетривиальные решения этой системы, т. к. вектор x должен быть отличен от нулевого. Это возможно тогда и только тогда, когда ранг матрицы системы (12.2) меньше числа неизвестных, что равносильно равенству нулю определителя матрицы этой системы, т. е.
| А – lЕ | 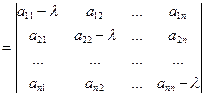 = 0. (12.3)
= 0. (12.3)
Определение 12.4. Равенство (12.3) называется характеристическим урав-нением матрицы А. Оно выражает условие, которому должны удовлетворять все собственные значения матрицы А. Левая часть характеристического уравнения (12.3) представляет собой многочлен степени n, называемый характеристическим многочленом матрицы А. Всякому его корню l 0 отвечает собственный вектор, координаты которого определяются из системы (12.2) после подстановки в нее вместо l величины l 0.
Приведем примеры нахождения собственных векторов и соответствующих им собственных значений для некоторых операторов.
Пример 1. Найти собственные значения и собственные векторы матрицы



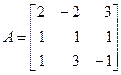 .
.
Решение. Составим характеристическое уравнение матрицы А и найдем его корни:
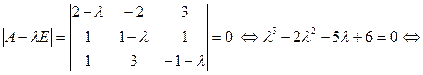
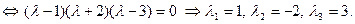
При l 1 = 1, согласно (12.2), получаем систему уравнений
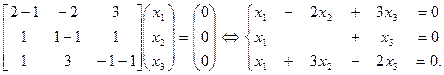
Из первых двух уравнений находим, что x 1 = – x 3 и x 2 = 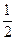 x 1 +
x 1 + 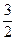 x 3 = x 3. Таким образом, значению l 1 соответствует собственный вектор (– x 3, x 3, x 3) = x 3(–1, 1, 1), где x 3 – произвольное ненулевое действительное число. В частности, при x 3 = 1 получим собственный вектор x 1 = (–1, 1, 1).
x 3 = x 3. Таким образом, значению l 1 соответствует собственный вектор (– x 3, x 3, x 3) = x 3(–1, 1, 1), где x 3 – произвольное ненулевое действительное число. В частности, при x 3 = 1 получим собственный вектор x 1 = (–1, 1, 1).
Аналогично, для l 2 = – 2 имеем
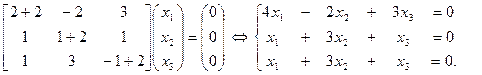
Из первых двух уравнений находим, что x 3 = –14 x 2, x 1 = 11 x 2, " x 2 Î R, x 2 ¹ 0. Таким образом, получаем собственный вектор вида x 2(11, 1, –14) || (11, 1, –14) = x 2.
Аналогично, для l 3 = 3 имеем
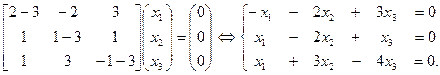
Отсюда x 1 = x 3, x 1 = x 2, или (x 1, x 2, x 3) = (x 1, x 1, x 1), " x 1 Î R, x 1 ¹ 0. То есть можно считать, что собственный вектор (x 1, x 1, x 1) || (1, 1, 1) = x 3.
Таким образом, у данной матрицы А собственные значения l 1 = 1, l 2 = – 2 и l 3 = 3, а соответствующие им нормированные собственные векторы имеют вид
v 1 = 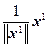 =
= 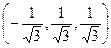 ; v 2 =
; v 2 = 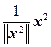 =
= 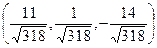 ; v 3 =
; v 3 = 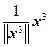 =
= 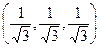 .·
.·
 2015-08-21
2015-08-21 9447
9447
