Изучим дополнительные свойства линейных операторов, связанные с понятием ортогональности в евклидовом пространстве. Вначале докажем следующее свойство: если A и B – линейные операторы, действующие в n -мерном евклидовом пространстве V, и (x, Ay) = (x, By),  x, y
x, y  V, то A = B.
V, то A = B.
В самом деле, положив в равенстве (x, Ay) = (x, By) Û (x, (A – B) y) = 0 вектор x = (A – B) y, получим ((A – B) y, (A – B) y) = ||(A – B) y ||2 = 0,  y
y  V, что равносильно равенству (A – B) y = 0,
V, что равносильно равенству (A – B) y = 0,  y
y  V, т. е. A – B = O, или A = B.
V, т. е. A – B = O, или A = B.
Определение 11.1. Линейный оператор A * называется сопряженным оператору A, если
(Ax, y) = (x, A * y),  x, y
x, y  V. (11.1)
V. (11.1)
Естественно возникает вопрос: существует ли для заданного оператора A сопряженный?
Теоремa 11.1. Каждый линейный оператор A имеет единственный сопряженный оператор A *.
Доказательство. Выберем в пространстве V ортонормированный базис u 1, u 2,…, u n. Каждому линейному оператору A: V ® V в этом базисе отвечает матрица А = 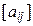 , i, j = 1, 2,..., n. Пусть
, i, j = 1, 2,..., n. Пусть 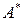 – матрица, полученная из матрицы А транспонированием. Ей соответствует линейный оператор B. Тогда
– матрица, полученная из матрицы А транспонированием. Ей соответствует линейный оператор B. Тогда
(Au j, u i) = (а 1 j u 1+ а 2 j u 2+…+ аnj u n, u i) = аij;
(u j, Bu i) = (u j, аi 1 u 1+ аi 2 u 2+…+ аin u n) = аij.
Откуда
(Au j, u i) = (u j, Bu i), i, j = 1, 2,..., n. (11.2)
Пусть далее x = x 1 u 1 + x 2 u 2 +…+ xn u n и y = у 1 u 1 + у 2 u 2 +…+ уn u n – любые два вектора из V. Рассмотрим скалярные произведения (Ax, y) и (x, By):
(Ax, y) = 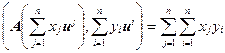 (Au j, u i),
(Au j, u i),
(x, By) = 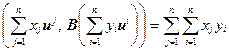 (u j, Bu i).
(u j, Bu i).
Сравнивая эти выражения с учетом равенства (11.2) и отмеченного выше свойства, получаем равенство (Ax, y) = (x, By),  x, y
x, y  V, т. е. B = A *.
V, т. е. B = A *.
Таким образом, доказано, что для каждого линейного оператора A в конечномерном евклидовом пространстве существует сопряженный ему оператор A *, матрица которого в любом ортонормированном базисе является транспонированной по отношению к матрице оператора A. Единственность оператора A * следует из определения сопряженного оператора и доказанного выше свойства.¨
Легко убедиться в том, что оператор A *, сопряженный линейному оператору A, является линейным.
Итак, оператор A * линеен и ему соответствует матрица A *. Поэтому соответствующее формуле (11.1) матричное соотношение имеет вид
(А x, y) = (x, A * y),  x, y
x, y  V.
V.
Сопряженные операторы обладают следующими свойствами:
1°. Е * = Е.
2°. (A *)* = A.
3°. (A + B)* = A * + B *.
4°. (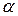 А)* =
А)* = 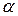 A *,
A *, 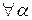
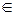 R.
R.
5°. (AB)* = B * A *.
6°. (A –1)* = (A *)–1.
Справедливость свойств 1°–5° вытекает из свойств транспонирования матриц.
Убедимся в справедливости свойства 6°. Пусть A –1 существует. Тогда из равенств AA –1 = A –1 A = Е и свойств 1°, 5° вытекает, что (AA –1)* = (A –1 A)* = Е * = = Е и (AA –1)* = (A –1)* A *, (A –1 A)* = A *(A –1)*, т. е. что (A –1)* = (A *)–1. Отсюда получаем еще одно важное свойство транспонирования матриц:
(A –1)* = (A *)–1.
Пример 1. Пусть A – поворот евклидовой плоскости R 2 на угол j с матрицей
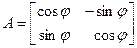
в ортонормированном базисе i, j. Тогда матрицей сопряженного оператора в этом базисе является
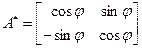 =
= 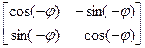 .
.
Следовательно, A * – поворот плоскости на угол j в противоположном направлении.·
 2015-08-21
2015-08-21 5448
5448
