Рассмотрим игру 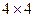 с матрицей
с матрицей
| А | В | ||||
| * | |||||
| 1* |
Отмечаем любую строку (например, первую) звездочкой в конце этой строки и перепишем эту строку под матрицей, и отметим звездочкой в ней наименьший элемент. На этом заканчивается первая ступень итеративного процесса. Число 1* стоит в третьем столбце, перепишем этот столбец справа от матрицы и отметим наибольшее число в нем звездочкой, т.е.5*:
| * | ||||||
| 5* | 6* | |||||
| 1* | ||||||
| 3* |
Число 5* находится во второй строке, сложите эту строку поэлементно со строкой, написанной под матрицей и отметьте звездочкой наименьшее число (3*) в новой строке. На этом заканчивается второй шаг. Так как число 3* стоит в первом столбце, складываем поэлементно этот столбец со столбцом справа от матрицы и отмечаем звездочкой наибольшее число, 6* (поскольку здесь несколько чисел принимают наибольшее значение, отмечать можно любое из них). Так как число 6* стоит во второй строке, сложим эту строку со строкой, расположенной в самом низу. На этом заканчивается третий шаг.
Если мы проведем десять таких шагов, получим такую картину:
| * | ||||||||||||||
| 5* | 6* | |||||||||||||
| 22* | 25* | 28* | ||||||||||||
| 10* | 14* | 16* | 18* | 20* | ||||||||||
| 1* | ||||||||||||||
| 3* | ||||||||||||||
| 4* | ||||||||||||||
| 8* | ||||||||||||||
| 11* | ||||||||||||||
| 13* | ||||||||||||||
| 15* | ||||||||||||||
| 17* | ||||||||||||||
| 20* | ||||||||||||||
| 23* | 24. |
Обратите внимание на то, что общее число звездочек под матрицей равно числу звездочек справа от матрицы. Теперь подсчитаем число звездочек в каждой строке и каждом столбце и напишем эти числа рядом с матрицей:
| 1 |
Эти числа дают приближенные оценки относительных частот, в соответствии с которыми игроки А и В должны смешивать свои чистые стратегии. Другими словами, 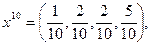 а
а 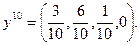 Легко установить по окончательной таблице, не проводя дополнительных вычислений, что
Легко установить по окончательной таблице, не проводя дополнительных вычислений, что 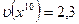 (как это сделать?), а
(как это сделать?), а 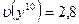 . Мы вправе заключить, что истинная цена игры
. Мы вправе заключить, что истинная цена игры 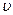 лежит между 2,3 и 2,8. Если продолжить итеративный процесс дальше (сделать 20 шагов), то можно найти лучшие смешанные стратегии: за игрока А это будет
лежит между 2,3 и 2,8. Если продолжить итеративный процесс дальше (сделать 20 шагов), то можно найти лучшие смешанные стратегии: за игрока А это будет 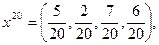 за В
за В 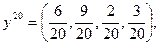 и средние выигрыши и проигрыши теперь будут в границах от
и средние выигрыши и проигрыши теперь будут в границах от 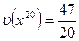 до
до 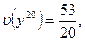 то есть от 2,35 до 2,65. Если этот результат не удовлетворяет требованиям, процесс можно продолжать сколь угодно долго. Для сравнения: точное решение нашей игры будет
то есть от 2,35 до 2,65. Если этот результат не удовлетворяет требованиям, процесс можно продолжать сколь угодно долго. Для сравнения: точное решение нашей игры будет 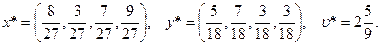
 2015-08-21
2015-08-21 372
372








