Данная матрица имеет седловую точку 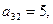 поэтому ее решением являются чистые стратегии
поэтому ее решением являются чистые стратегии 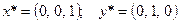 при
при 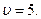 Однако мы найдем решение этой игры указанным выше общим методом. Пара двойственных задач будет в данном случае выглядеть следующим образом:
Однако мы найдем решение этой игры указанным выше общим методом. Пара двойственных задач будет в данном случае выглядеть следующим образом:
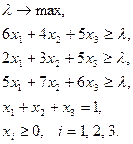
| 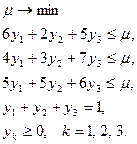
|
В силу того, что все элементы матрицы 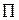 положительны (заметим, что любая матричная игра может быть эквивалентно преобразована так, чтобы элементы матрицы стали положительны), ясно, что
положительны (заметим, что любая матричная игра может быть эквивалентно преобразована так, чтобы элементы матрицы стали положительны), ясно, что 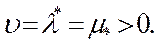 Поэтому нам можно преобразовать эти задачи к более удобному для решения виду. Именно, введем новые переменные по формулам:
Поэтому нам можно преобразовать эти задачи к более удобному для решения виду. Именно, введем новые переменные по формулам:
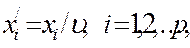 (1.33)
(1.33)
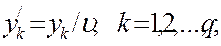 (1.34)
(1.34)
тогда, очевидно, наши задачи будут эквивалентны следующим:
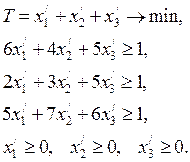
| 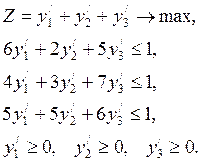
|
Решив эти задачи, найдем 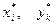 из соотношений:
из соотношений:
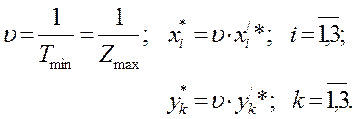 (1.35)
(1.35)
Решим вторую из задач симплекс-методом:
 Таблица 1.4 Таблица 1.4
| Таблица 1.5 | |||||||||
| Базис перем. | 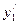
| 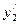
| 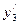
| Свободные члены | Базис перем. | 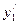
| 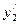
| 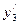
| Свободные члены | |
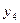
| 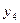
| -2/5 | 13/5 | 3/5 | ||||||
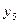
| 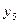
| -3/5 | 17/5 | 2/5 | ||||||

| 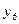
| 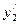
| 1/5 | 6/5 | 1/5 | |||||
| Z | -1 | -1 | -1 | Z | 1/5 | 1/5 | 1/5 |
После первой же итерации получаем оптимальное решение 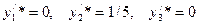 и
и 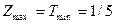 . Отсюда получаем
. Отсюда получаем 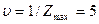 и
и 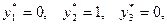 т.е.
т.е. 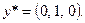 По таблице 1.5 из теории двойственности получаем оптимальное решение первой задачи
По таблице 1.5 из теории двойственности получаем оптимальное решение первой задачи 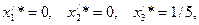 отсюда
отсюда 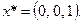
 2015-08-21
2015-08-21 248
248








