Итеративный метод Брауна - Робинсон

Точные методы, которые рассмотрены в предыдущем параграфе, легко обобщаются теоретически на матричные игры любой размерности. Однако применение этих методов даже для решения небольших игр, в которых число стратегий игроков лежит в пределах от 4 до 10, требует применения слишком большого числа вычислений. Например, в игре 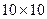содержится более 40000 игр типа 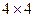. Если же поставить задачу отыскания приближенного решения игры, то оказывается, существуют достаточно простые и в то же время эффективные методы ее решения. В этом пункте мы остановимся на итеративном методе Брауна - Робинсон, называемом еще методом фиктивного разыгрывания.

Предположим, что два игрока решают разыграть игру много раз, следя при этом за чистыми стратегиями, которые использует противник в отдельных разыгрываниях игры. При N разыгрывании каждый игрок действует так, чтобы максимизировать свой ожидаемый выигрыш против наблюдаемого эмпирического вероятностного распределения противника, если игрок В использовал свою k -ю стратегию 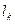раз, то игрок А выбирает i так, чтобы максимизировать 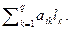Аналогично, если игрок А использовал i -ю стратегию 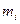раз, то игрок В выберет k так, чтобы минимизировать .

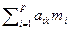Оказывается, такие эмпирические распределения сходятся к оптимальным стратегиям. Точнее, пусть 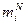- число использований игроком А i -й стратегии в течение первых N разыгрываний игры. Если положить 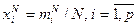, то очевидно, что 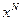является смешанной стратегией. Эта последовательность стратегий не обязана сходиться, но справедливо утверждение, что предел любой сходящейся подпоследовательности является оптимальной стратегией. При этом, если мы обозначим 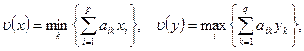то будет выполнено следующее равенство

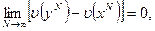(1.20)

которое позволяет приближенно находить цену игры.

Как уже упоминалось, этот метод наиболее полезен в случае очень больших игр, к которым довольно трудно применять какой-либо другой метод вследствие их объема.