Пусть дана грамматика G = (N, T, P, S). Тогда если правила грамматики не удовлетворяют никаким ограничениям, то ее называют грамматикой типа 0, или грамматикой без ограничений.
Если каждое правило грамматики, кроме S 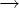 e, имеет вид
e, имеет вид 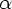
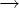
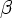 , где |
, где | 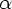 |
| 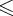 |
| 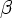 |, и в том случае, когда S
|, и в том случае, когда S 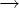 e
e 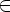 P, символ S не встречается в правых частях правил,то грамматику называют грамматикой типа 1, или неукорачивающей.
P, символ S не встречается в правых частях правил,то грамматику называют грамматикой типа 1, или неукорачивающей.
Если каждое правило грамматики имеет вид A 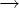
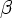 , где A
, где A 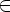 N,
N, 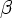
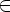 (N
(N 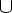 T)*, то ее называют грамматикой типа 2, или контекстно-свободной (КС-грамматикой).
T)*, то ее называют грамматикой типа 2, или контекстно-свободной (КС-грамматикой).
Если каждое правило грамматики имеет вид либо A 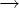 xB, либо A
xB, либо A 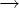 x, где A, B
x, где A, B 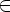 N, x
N, x 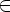 T* то ее называют грамматикой типа 3, или праволинейной.
T* то ее называют грамматикой типа 3, или праволинейной.
Язык типа 1 - контекстно-зависимым (КЗ), язык типа 2 - контекстно-свободным (КС), язык типа 3 - праволинейным.
K3 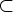 K2
K2 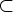 K1
K1 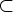 K0.
K0.
Грамматика G называется неоднозначной, если существует цепочка w, для которой имеется два или более различных деревьев вывода в G.
Грамматика G называется леворекурсивной, если в ней имеется нетерминал A такой, что существует вывод 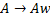 для некоторой цепочки w.
для некоторой цепочки w.
Атрибутной грамматикой называется четверка AG = (G, AS, AI, R), где
· G = (N, T, P, S) - приведенная КС-грамматика;
· AS - конечное множество синтезируемых атрибутов;
· AI - конечное множество наследуемых атрибутов, AS 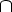 AI =
AI = 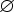 ;
;
· R - конечное множество семантических правил.
Атрибутная грамматика AG сопоставляет каждому символу X из N 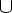 T множество AS(X) синтезируемых атрибутов и множество AI(X) наследуемых атрибутов.
T множество AS(X) синтезируемых атрибутов и множество AI(X) наследуемых атрибутов.
 2015-08-21
2015-08-21 301
301








