Квазиньютоновский метод

Описание алгоритма:

Данный метод обладает положительными чертами метода Ньютона, однако, использует информацию только о первых производных. В этом методе приближение к очередной точке в пространстве оптимизируемых параметров задается формулой:

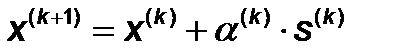
Направление поиска определяется выражением:

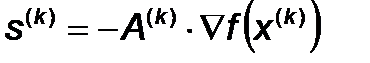, где 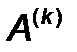- матрица порядка 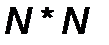(метрика).

Матрица 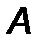- вычисляется по формуле.

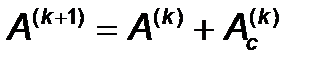, где:

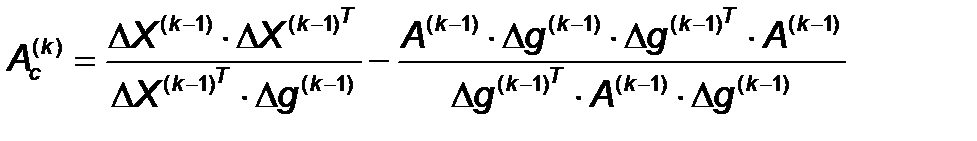
Где 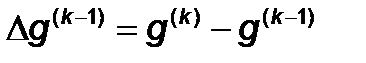изменение градиента на предыдущем шаге.

Данный алгоритм отличается устойчивостью, так как обеспечивает убывание целевой функции от итерации к итерации.

Алгоритм метода:

Шаг 1. Задать: начальную точку х⁽⁰⁾. Перейти к шагу 2.

Шаг 2. Вычислить направление поиска s^(k). Перейти к шагу 3.

Шаг 3. Произвести поиск вдоль прямой 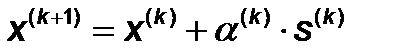. Перейти

к шагу 4.

Шаг 4. Проверка условия окончания поиска.

Да: закончить поиск;

Нет: перейти к шагу2.

Ход решения:

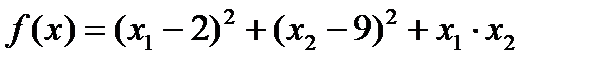
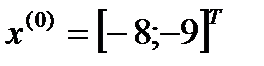
Шаг 1.

Положим .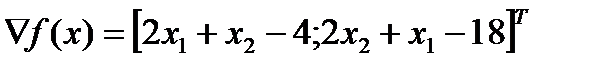

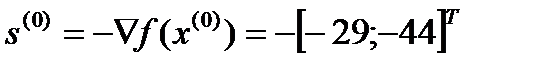
Шаг 2. Поиск вдоль прямой приводит к результату, полученному в предыдущем методе:

.

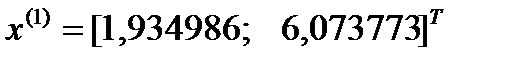Шаг 3.

,

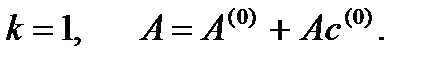
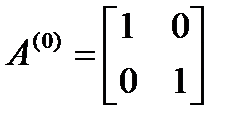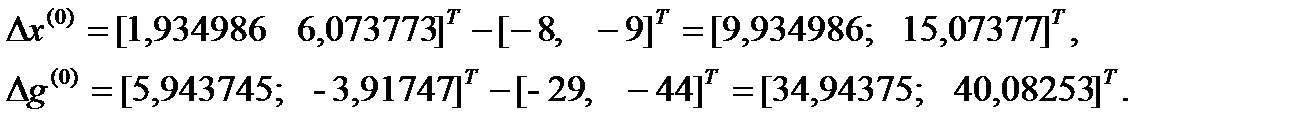
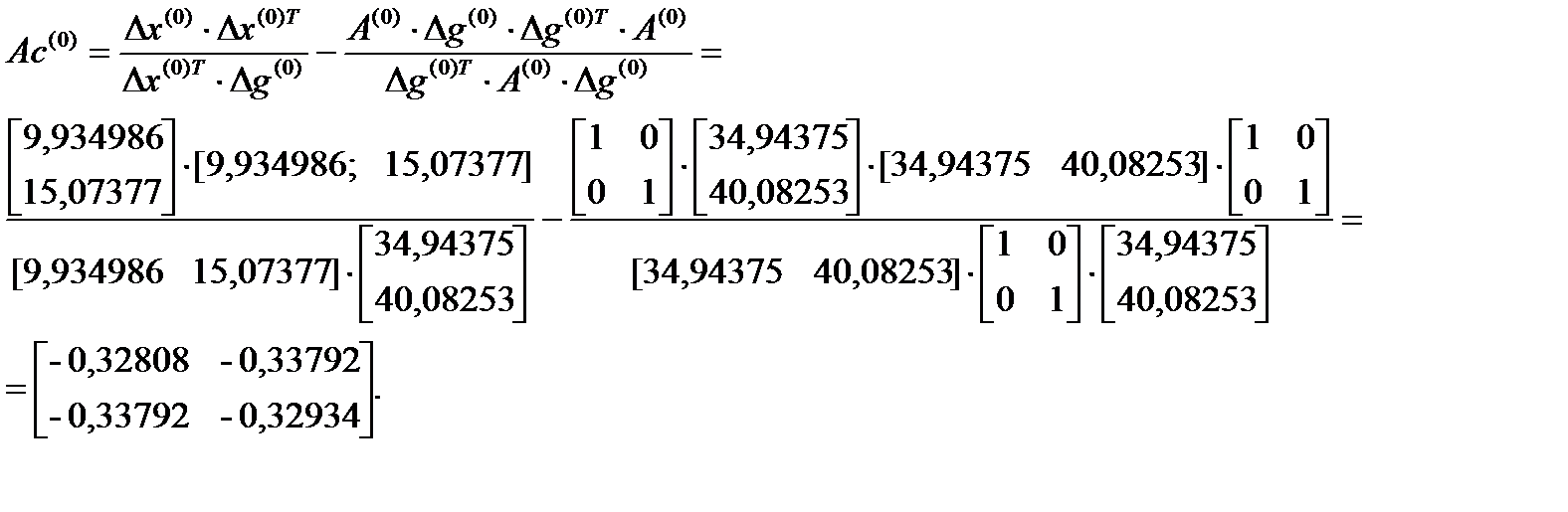
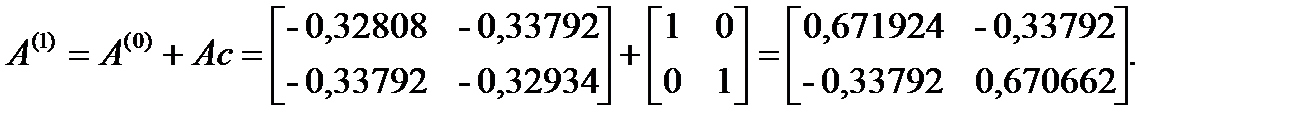
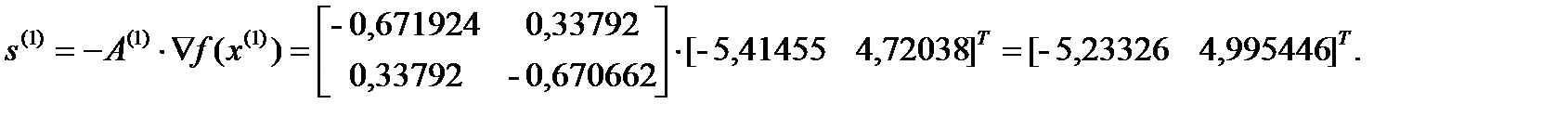
Шаг 4. Поиск вдоль прямой.

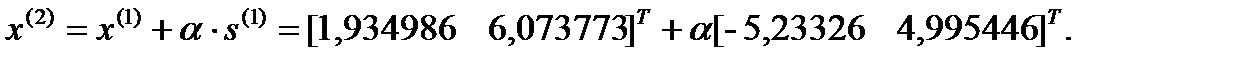
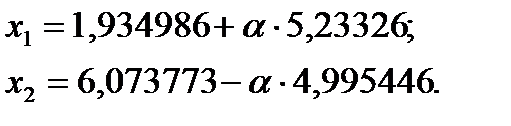
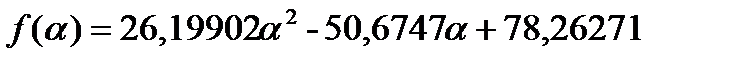
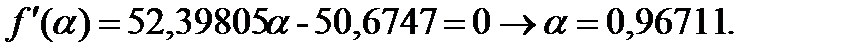
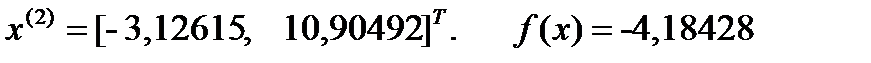
Решение поставленной задачи квазиньтоновским методом представлено на рисунке 7.

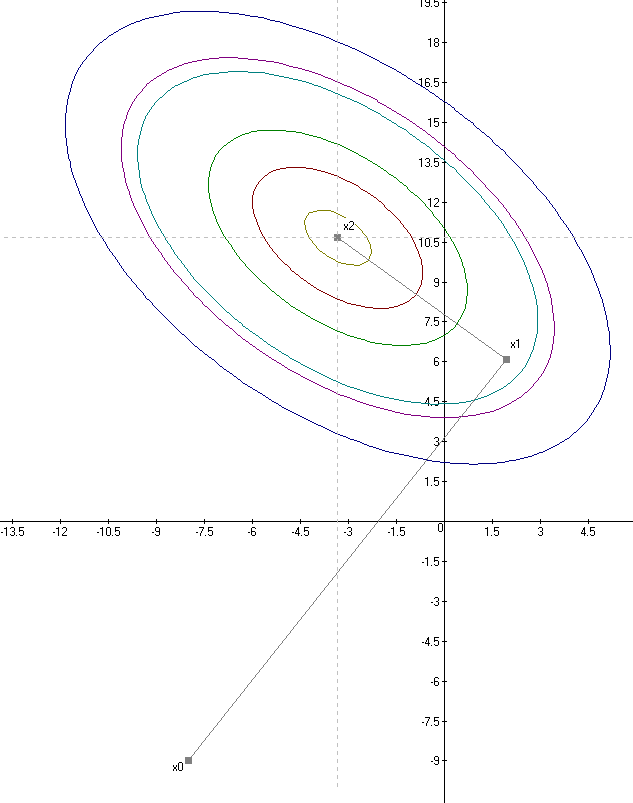Рисунок 7 – решение задачи квазиньтоновским методом