Сторонние источники. Уравнения Максвелла с учётом таких источников.
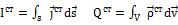 Являются первопричиной поля.
Являются первопричиной поля.
1-ое: 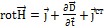 3-e:
3-e: 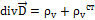
В случае переменных полей 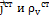 связаны уравнением непрерывности
связаны уравнением непрерывности
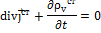
Закон Ома в дифференциальной форме
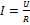
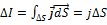
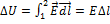
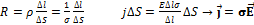 ,где
,где 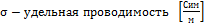
Уравнение непрерывности. Закон сохранения заряда.
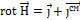
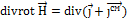
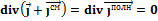
Линии полного тока всегда замкнуты (непрерывны).
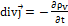 по теореме Гаусса
по теореме Гаусса 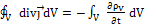
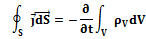
Классификация сред по их макроскопическим параметрам: линейный и нелинейные, однородные и неоднородные, изотропные и анизотропные.
Нелинейные: 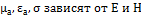
Линейные: 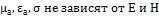
Однородные: 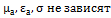 от координат
от координат
Неоднородные: 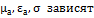 от координат
от координат
Изотропные: свойства среды одинаковы по разным направлениям
Анизотропные: свойства среды различны по разным направлениям
Неприменимость уравнений Максвелла в дифференциальной форме на границе раздела двух сред.
Дифференциальные уравнения Максвелла неприменимы на границах раздела сред. Здесь поля не дифференцируемы по координатам и операторы div и rot в обычном смысле не существуют. В окрестности границы поля связаны граничными условиями для их нормальных и касательных проекций. Эти условия выводятся из интегральных уравнений Максвелла.
11. Вывод граничных условий для нормальных составляющих векторов 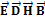 .
.
Соотношения, показывающие связь между значениями составляющих векторов электромагнитного поля в разных средах у поверхности раздела, называют граничными.
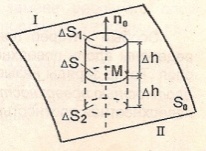 Применим третье уравнение Максвелла в интегральной форме к объему цилиндра ∆V, ограниченного поверхностями ∆S1 и ∆S2 и ∆S
Применим третье уравнение Максвелла в интегральной форме к объему цилиндра ∆V, ограниченного поверхностями ∆S1 и ∆S2 и ∆S
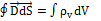 элемент dS направлен по внешней нормали к поверхности
элемент dS направлен по внешней нормали к поверхности 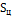 , поэтому
, поэтому 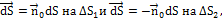
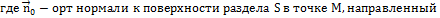
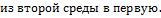 Устремляя ∆h к нулю (при этом
Устремляя ∆h к нулю (при этом 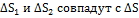 )
)
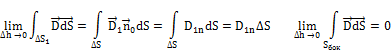
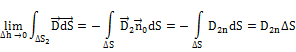
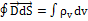
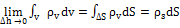
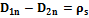
Соотношение показывает, что 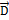 претерпевает разрыв, равный плотности поверхностных зарядов.
претерпевает разрыв, равный плотности поверхностных зарядов.
Выражая в этом соотношении 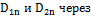
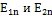 c помощью равенства
c помощью равенства 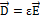 , полоучаем граничное условие для
, полоучаем граничное условие для 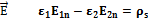
Соотношение показывает, что 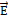 претерпевает разрыв, равный отношению диэлектрических проницаемостей этих сред.
претерпевает разрыв, равный отношению диэлектрических проницаемостей этих сред.
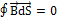
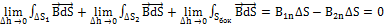
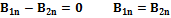
Соотношение показывает, что 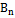 непрерывна при переходе через границу раздела двух сред.
непрерывна при переходе через границу раздела двух сред.
Из соотношения 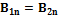 получим
получим 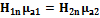 , т.к
, т.к 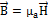
12. 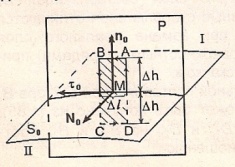 Вывод граничных условий для касательных составляющих векторов
Вывод граничных условий для касательных составляющих векторов 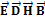 .
.
Граничные условия могут быть получены из первого и второго уравнений Максвелла в интегральной форме.
Применим к контуру ABCD первое уравнение Максвелла
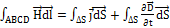 ,
, 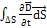 =0,
=0, 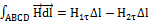
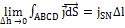 , следовательно
, следовательно 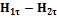 =
= 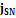 , если на границе раздела отсутствуют поверхностные токи, то правая часть равенства равна нулю и
, если на границе раздела отсутствуют поверхностные токи, то правая часть равенства равна нулю и 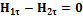
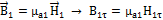
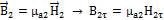
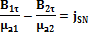
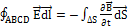 ,
,
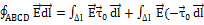 )
) 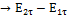
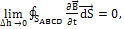 следовательно
следовательно 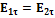
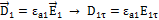
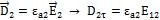
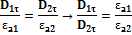
 2015-08-21
2015-08-21 1115
1115







