Обобщенный метод Крамера-Лагранжа

Особенность 2-го, 6-го и 7-го элементов в том, что они лишь частично образуются координатными поверхностями системы. Поскольку число их узлов 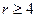, применять к ним универсальный метод Крамера нецелесообразно. Возможен другой, более эффективный способ, сочетающий методы Крамера и Лагранжа.

Введем иерархию элементов, подразделив их на порождающие с 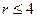, и порождаемые с 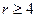. Порождение элемента можно осуществить трансляциейпорождающего элемента в общем случае в произвольном направлении, или его поворотом вокруг некоторой оси на угол 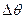– для ограниченно симметричных, или на 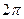– для осесимметричных элементов. В результате размерность порожденного элемента увеличится на единицу.

Так как порождающий элемент не образован координатными поверхностями, то его базисные функции находятся методом Крамера при 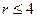, а затем к нему применяется метод Лагранжа, который равнозначен операциям трансляции или поворота. В силу этого, достаточно базисные функции порождающего двумерного элемента умножить на полином Лагранжа 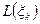в направлении орта трансляции, чтобы получить базисные функции порожденного объемного элемента :

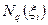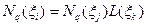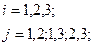
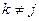, . (4.3.1)

Применяя обобщенный метод Крамера-Лагранжа ко второму элементу каталога, для его базисных функций получим следующее выражение:

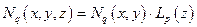, при 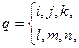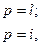(4.3.2)

где 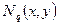– базисные функции (4.1.7) треугольного элемента; а полиномы Лагранжа равны:

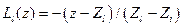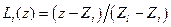; . (4.3.3)

Эти же формулы описывают и седьмой элемент базового каталога, если в

базисных функциях переменные 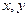заменить на 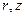, а в полиноме Лагранж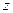а – на :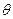

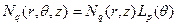. (4.3.4)

У шестого элемента на полиномы Лагранжа 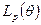умножаются лишь базисные функции узлов 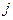и .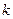

Все полностью симметричные элементы базового каталога относятся к порожденным поворотом на 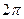порождающих их двумерных элементов. В силу того, что при этом 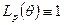, базисные функции порожденных и порождающих их элементов идентичны.