Метод Крамера

Математическое описание элемента можно получить тремя способами. В этом параграфе приведен первый, как наиболее общий.

Для наглядности рассмотрение проведем на конкретном примере двумерного треугольного элемента с тремя узлами (см. рис. 4.1).

Представим приближенное решение для элемента полиномом 1-го ранга с

неизвестными коэффициентами :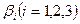

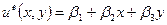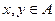, . (4.1.1)

Подставляя в (4.1.1) координаты узлов и получаемые в результате значения функции в каждом из узлов – 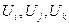, соответственно, получим систему уравнений (4.1.2) для определения :

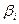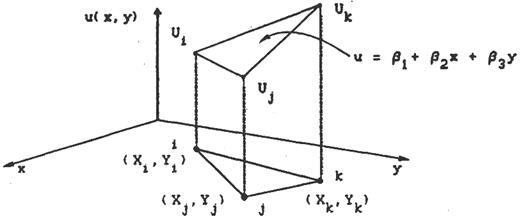
Рис. 4.1

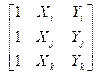
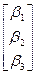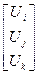= , (4.1.2)

решение которой можно получить методом Крамера.

Определитель этой системы уравнений равен 2А – удвоенной площади элемента [11]:

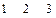
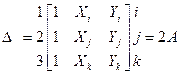. (4.1.3)

Запишем в развернутом виде решение системы (4.1.2) на языке алгебраических дополнений:

; ;

.

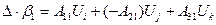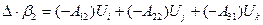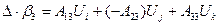Подставим найденные значения 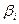в (4.1.1) и сгруппируем члены, умножаемые на узловые значения функции U_q (q=i,j,k):

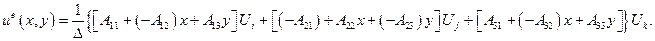
Выражения в квадратных скобках зависят от координат узлов элемента и текущих переменных 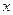и 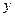. Их принято называть функциями формы, базисными или интерполяционнымифункциями элемента. Представим их в общем виде:

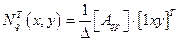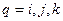, . (4.1.4)

Элементами матрицы 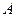_qp служат алгебраические дополнения 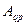определителя (4.1.3):

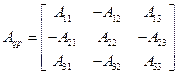
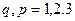(4.1.5)

и являются определителями 2-го порядка.

Более удобной является несколько иная форма записи базисных функций:

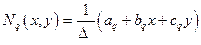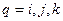; . (4.1.6)

Сопоставляя последнее выражение с (4.1.4) и (4.1.5), видим, что коэффициенты 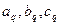– это столбцы матрицы (4.1.5) при фиксированном 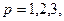соответственно;

при фиксированном 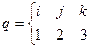это элементы соответствующей строки этой же матрицы. Например, пр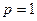и и 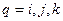получим:

, , ;

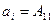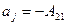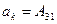пр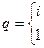и и 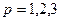для базисной функции будем иметь:

.

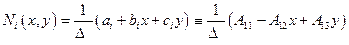Раскрывая алгебраические дополнения, найдем конкретные выражения коэффициентов через координаты узлов элемента:

a_i = X_jY_k – X_kY_j; a_j = X_kY_i – X_iY_k; a_k = X_iY_j – X_jY_i;

b_i = Y_j – Y_k; b_j = Y_k – Y_i; b_k = Y_i – Y_j; (4.1.7)

c_i = X_k – X_j; c_J = X_i – X_k; c_k = X_j – X_i.

Переход к другим системам координат осуществляется заменой текущих переменных 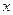, 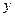: в цилиндрической – на 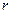, 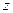; в сферической – на 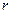и .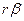

С введением понятия базисной функции аппроксимирующую функцию (4.1.1) (или (4.1.4)) можно представить как явную функцию ее узловых значений :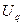

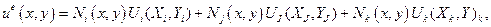(4.1.8а))

или в матричной форме:

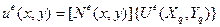, (4.1.8б))

где [ 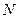^e(x,y) ] – матричная строка базисных функций; { 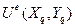} – вектор-столбец значений функций в узлах элемента.

Степень аппроксимирующего полинома определяет число узлов, которым должен обладать элемент, – оно должно равняться числу неизвестных коэффициентов 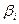, входящих в полином. Например, если вместо (4.1.1) взять полином 2-ой степени:

,

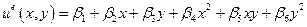то для определения 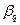элемент должен содержать шесть узлов – q =1,2…..6.

Располагать дополнительные узлы следует на сторонах треугольника, желательно (но не обязательно) в их серединах, как показано на рис. 4.2. Элементы с полиномом 2-ой степени называют квадратичными, 3-ей степени - кубичными и т.д. Находить базисные функции этих элементов очень сложно, так как для этого необходимо раскрывать определители q-го порядка.

Если дополнительные узлы соединить прямыми, то треугольный элемент разобьется на четыре треугольные подобласти меньшего размера. Замена квадратичного элемента четырьмя линейными существенно упрощает математическую процедуру

отыскания решения, – система уравнений становится линейной.

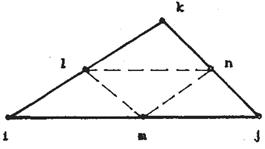
Рис. 4.2 Расположение дополнительных узлов на сторонах элемента

Аппроксимирующую функцию (4.1.1) для двумерного треугольника легко обобщить на трехмерный элемент – тетраэдр – добавлением третьей – z-ой координаты:

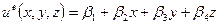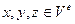, . (4.1.9)

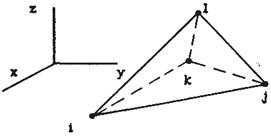
Рис. 4.3

Из вида (4.1.9) следует, что формулы для тетраэдра получаются, минуя все

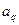
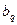
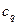
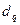
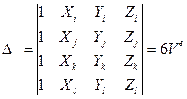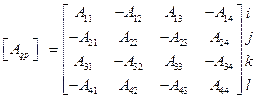; ; (4.1.10)

процедуры, из формул для треугольника простым увеличением на единицу порядка определителя (4.1.3) и ранга матрицы (4.1.5). При этом элементы 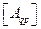– алгебраические дополнения определителя 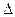, становятся определителями 3-го порядка.

Базисные функции тетраэдра будут иметь вид, аналогичный функциям треугольного элемента (4.1.4) или (4.1.6):

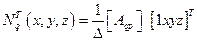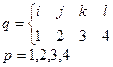, , (4.1.11)

или

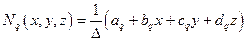. (4.1.12а))

Формула интерполяционной функции для тетраэдра имеет вид:

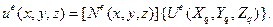(4.1.12б))

Описанный первый способ получения базисных функций, основанный на решении уравнений методом Крамера, удобен для простых, так называемых симплекс-

элементов, допускающих использование полинома первого порядка. Число узлов симплекс-элементов на единицу больше его размерности, т.е. минимально возможное. Для элементов, контуры которых не совпадают с координатной сеткой системы, первый способ является единственно возможным.