Достоинство первого способа состоит в его применимости к любым элементам независимо от их размерности и количества узлов. С его помощью при известном в явном виде аппроксимирующем полиноме 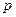 -го ранга базисные функции в принципе всегда могут быть найдены, так как матрица типа (4.1.2) обратима, поскольку ее определитель (4.1.3) отличен от нуля, – площадь или объем элемента никогда не равны нулю. Универсальность метода Крамера нивелируется его неэффективностью при числе узлов элемента
-го ранга базисные функции в принципе всегда могут быть найдены, так как матрица типа (4.1.2) обратима, поскольку ее определитель (4.1.3) отличен от нуля, – площадь или объем элемента никогда не равны нулю. Универсальность метода Крамера нивелируется его неэффективностью при числе узлов элемента 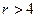 .
.
К элементам, образованным координатными линиями, целесообразно применять более простой метод Лагранжа.
Рассмотрим аппроксимацию функции 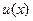 полиномом
полиномом 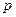 -го ранга, считая, что значения функции заданы как
-го ранга, считая, что значения функции заданы как 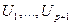 в
в 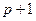 точках
точках 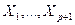 . Из численного анализа известно, что функция
. Из численного анализа известно, что функция 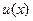 может быть задана как полином
может быть задана как полином 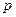 -ой степени:
-ой степени:
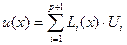 , (4.2.1)
, (4.2.1)
где 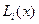 – полином Лагранжа, определяемый равенством:
– полином Лагранжа, определяемый равенством:
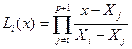 . (4.2.2)
. (4.2.2)
Если под 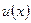 понимать аппроксимирующую элементную функцию
понимать аппроксимирующую элементную функцию 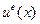 , то из сопоставления (4.2.1) с (2.2.1) видно, что полиномы Лагранжа – это базисные функции элемента, а базовые точки
, то из сопоставления (4.2.1) с (2.2.1) видно, что полиномы Лагранжа – это базисные функции элемента, а базовые точки 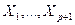 – координаты его узлов, или узловые точки.
– координаты его узлов, или узловые точки.
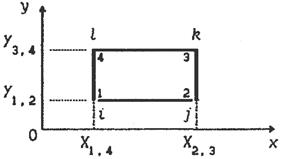
Проиллюстрируем метод Лагранжа на примере изображенного на рис. 4.4 элемента, образованного координатными линиями декартовой системы [4].
Использование равенств (4.2.1) и (4.2.2) на стороне 1–2 (y=const), позволяет определить u(x) на этой стороне:
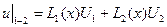 ,
,
где 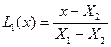 ;
; 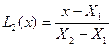 ;
;
Аналогично на стороне 4–3 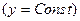 получим:
получим:
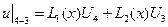 .
.
Применяя эти же рассуждения для сторон с 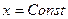 , найдем:
, найдем:
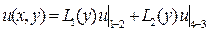 , где
, где 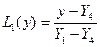 ;
; 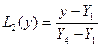 .
.
Собирая полученные выражения, для аппроксимирующей функции элемента будем иметь:
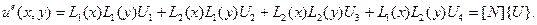
Видно, что попарные произведения полиномов Лагранжа соответствуют базисным функциям элемента:
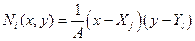 ;
; 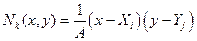 ;
;
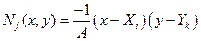 ;
; 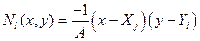 .
.
Здесь 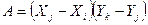 – площадь элемента.
– площадь элемента.
Обобщая эти соотношения на трехмерный элемент – координатную ячейку, придем к его математическому описанию в виде произведения трех лагранжевых полиномов, справедливому при любом 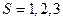 :
:
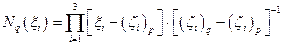 , p ≠ q, (4.2.4)
, p ≠ q, (4.2.4)
где ξi – текущая переменная; ζi – координаты q -го и p -го узлов; p – индексы узлов, с которыми узел q расположен на координатных поверхностях 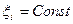 .
.
Как следует из (4.2.4), методом Лагранжа легко получить базисные функции всех элементов каталога, кроме второго, шестого и седьмого.
 2015-08-21
2015-08-21 563
563








