2015-08-21
691
Полученное в п. 6.2 выражение (6.2.10) является решением линейного уравнения теплопроводности с линейными граничными условиями, так как все теплофизические параметры задачи полагались постоянными. Это ограничение общности решения может быть снято программными методами [1].
При небольшой величине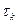 
временного шага изменения температуры на 
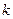- ом шаге будут невелики, в силу чего параметры задачи можно считать постоянными на этом временном элементе. Это тем более справедливо, если учесть, что температурная зависимость параметров довольно слабая – 
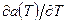(через а обозначен теплофизический параметр) невелико. Однако постепенно изменения температуры будут накапливаться и на каком-то временнόм шаге значения параметров следует перевычислить соответственно средней температуре элемента по заложенной в физическом каталоге процедуре:
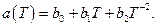(6.3.1)
Здесь под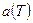 
понимаются: коэффициент теплопроводности 
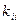; объемная теплоемкость 
; 
.
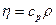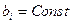Для установления момента времени, в который нужно производить перерасчет параметров, на каждом шаге 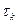, начиная с 
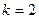, достаточно сравнить среднеобъемную температуру элемента (см.(5.4.1)) с ее значением на первом временном отрезке:
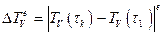. (6.3.2)
По задаваемой величине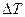 
, например, ≈ 100К, можно теперь определить номер к - го временнόго шага, с которого нужно перевычислить по (6.3.1) параметры тех элементов e ′, для которых условие 
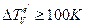оказалось выполненным. Для этих элементов находятся разности:
,
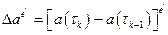и в стандартизованных матрицах элементов e ′ 
коэффициенты 
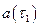заменяются на 
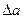, что позволяет найти поправочные числовые матрицы 
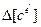и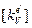 
.Все найденные указанным способом поправочные матрицы заносятся по известной процедуре (см. п. 5.2) в глобальные матрицы 
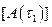и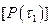 
, что приводит к поправленным на температурную зависимость параметров матрицам 
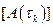и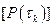 
. Относительно поправки объемной теплоемкости следует иметь в виду, что температурная зависимость ср и ρ носит противоположный характер: если ср растет с температурой, то ρ – падает, так что их произведение крайне слабо зависит от температуры. Поэтому поправлять матрицу теплоемкости на температурную зависимость едва ли целесообразно.
В отличие от глобальных матриц, глобальный вектор тепловой нагрузки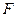 
формируется на каждом временнόм элементе, поскольку в общем случае:
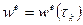и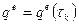 
.
Поверхностная его часть определяется комплексным коэффициентом
,
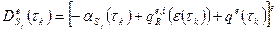который так же находится на каждом .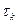
Таким образом, рекуррентное уравнение (6.2.10) с внесенными поправками на температурную зависимость параметров, по которому нужно проводить расчет температур на следующем–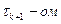 
шаге, будет иметь вид [1]:
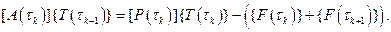(6.3.3)
На последующих временных шагах температура "поправленных"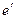 
элементов сравнивается с их же температурой на 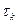шаге, а температура остальных 
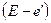элементов – с их температурой на 
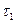шаге. Следовательно, неравенство (6.3.2) после 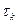- го шага расщепляется на два неравенства:
,
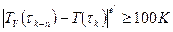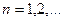(6.3.4)
.
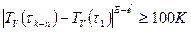При выполнении любого из них процедура внесения поправок повторяется.
