Остановимся кратко на некоторых вопросах математического характера.
Обычно решение, полученное методом конечных элементов, является приближением к истинному, или точному решению. Как близко это вычисленное решение к точному, и сходится оно или нет – это два важных вопроса, требующих ответа. Попытаемся оценить точность и сходимость метода конечных элементов.
Точность – это мера близости численного решения к точному, или истинному. Устойчивость определяется ростом ошибок при выполнении отдельных вычислительных операций. Неустойчивое вычисление является результатом аппроксимации, округления или других ошибок, которые неограниченно накапливаются, вследствие чего истинное решение тонет в ошибках. Сходимость – это постепенное приближение последовательно вычисляемых решений к предельному по мере того, как уточняются некоторые вычислительные параметры, такие, как размер элемента или ранг базисной функции в пробном решении. Термин “сходимость“ в этом же смысле применяется и к итерационной процедуре, в которой некоторые или все результаты одного вычисления становятся входной информацией для другого (повторного) вычисления. В сходящейся процедуре разница между последовательными результатами уменьшается, стремясь в пределе к нулю. Более подробные сведения по этим вопросам можно найти в курсах по численному анализу и методам вычислений.
В добавление к обычным ошибкам округления и аппроксимации, связанным с какой-либо вычислительной процедурой, есть и ошибки, связанные с самим методом конечных элементов. К ним относятся:
• ошибки дискретизации, являющиеся результатом геометрических различий границы области и ее аппроксимации по методу конечных элементов;
• ошибки пробной, или базисной функции, обусловленные разностью между точным решением и его представлением пробной функцией.
Ошибки дискретизации могут быть уменьшены использованием более мелких элементов или расположением криволинейных около границы. Ошибки пробной функции не обязательно уменьшаются по мере уменьшения размера элемента и могут поэтому мешать сходимости к точному решению или даже приводить к расходимости.
В общем случае полиномиальная пробная функция может только тогда дать точное решение на элементе конечного размера, когда полином является полным и имеет бесконечную степень. Последовательность линейно независимых функций считается полной, если можно найти такое число N и набор постоянных аi, при которых для произвольной допустимой функции u того же пространства R справедливо неравенство
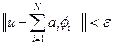
для любой наперед заданной величины ε. Поскольку на практике возможно использовать конечное число членов, представление пробной функции в виде полинома не может быть ничем иным, как приближением к точному решению. Это означает, что на элементе конечного размера пробная функция в виде полинома конечной степени всегда содержит ошибку.
Элементный вклад (5.1.5) содержит функцию 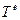 и ее производные до порядка n включительно. Полиномиальное представление для
и ее производные до порядка n включительно. Полиномиальное представление для 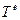 должно содержать, как минимум, степень n, если n-я производная отлична от нуля. Выбирая полиномы n-ой степени, получим в пределах элемента следующие представления:
должно содержать, как минимум, степень n, если n-я производная отлична от нуля. Выбирая полиномы n-ой степени, получим в пределах элемента следующие представления:
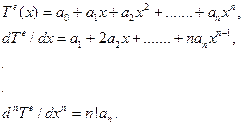 (6.4.1)
(6.4.1)
Отсюда видно, что, поскольку полином для 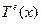 является полным, каждая из производных имеет в своем представлении член, не зависящий от х. По мере того, как размер элемента стремится к нулю, каждая из производных стремится к своему точному значению, и, следовательно, также ведет себя и элементный вклад. В результате процедура сходится.
является полным, каждая из производных имеет в своем представлении член, не зависящий от х. По мере того, как размер элемента стремится к нулю, каждая из производных стремится к своему точному значению, и, следовательно, также ведет себя и элементный вклад. В результате процедура сходится.
Вышесказанное позволяет сформулировать критерий 1 ограниченной
сходимости: условием сходимости является представление переменной внутри элемента в виде полного полинома как минимум степени n, где n – наивысший порядок производной в определяющем (ключевом) интеграле (5.1.5).
Когда для представления переменной 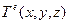 используется полином более высокой степени, чем указанный минимум, от аппроксимации можно ожидать большей точности и меньшей ошибки пробной функции и, как следствие, более высокой скорости сходимости.
используется полином более высокой степени, чем указанный минимум, от аппроксимации можно ожидать большей точности и меньшей ошибки пробной функции и, как следствие, более высокой скорости сходимости.
Наряду с понятием полноты, вводится еще одна характеристика пробной функции, – согласованность. Пробная функция рассматривается как согласованная, если переменная и ее производные вплоть до порядка n-1 непрерывны при переходе через границу между элементами, где n – порядок самой высокой производной в ключевом интеграле (5.1.5) для элементного вклада. Это позволяет сформулировать критерий 2 ограниченной сходимости: условие сходимости состоит в том, что элементы должны быть согласованными, т.е. при переходе через границу между элементами должны быть непрерывны сама функция и ее производные вплоть до порядка n-1 включительно. Отсюда следует, что квадратичные и более высокого порядка элементы, будучи, согласно определению, согласованными, безусловно обеспечивают сходимость метода конечных элементов в версии как метода Галеркина, так и вариационного. Для одного и того же класса задач критерии 1 и 2 являются достаточными условиями сходимости метода конечных элементов независимо от его формулировки.
Существует еще один критерий 3 сходимости, связанный с размером элемента, а именно, условие сходимости состоит в том, что по мере стремления к нулю размера элемента, члены с производными и функцией в уравнениях должны стремиться к функции той гладкости, что и точное решение в предположении непрерывности последней.
Из изложенного выше может сложиться впечатление, что все типы элементов, для которых гарантируется сходимость, одинаково полезны. Это не совсем так, поскольку на практике очень важна еще и точность. Как можно
практически оценить вычисленного решения? Если иметь в виду общий случай, то, к сожалению, никак. Одним из двух способов, однако, часто можно получить достаточный показатель точности.
Первый из них очевиден: путем сопоставления с известным аналитическим решением.
Второй метод требует предварительного определения типа сходимости для конкретной формулировки МКЭ и для конкретной задачи. Если окажется, что сходимость улучшается монотонно по мере уменьшения размеров элемента, то можно решать задачу несколько раз с последовательно уменьшаемыми элементами, и для получения решения экстраполировать результаты.
Монотонная сходимость МКЭ к точному имеет место, если:
• тип элемента удовлетворяет условиям полноты и согласованности по
критериям 1 и 2;
• размеры сетки уменьшаются таким образом, чтобы элементы каждого
последующего уровня представляли собой части соответствующих
элементов предыдущего уровня;
• подмножество разбиений каждого уровня содержится в подмножествах
предыдущего уровня.
Представление зависимой переменной на элементе не должно зависеть от используемой системы координат, или, точнее, должно быть геометрически инвариантным для ортогональных преобразований системы координат. Это принято называть пространственной, или геометрической изотропией. Кроме инвариантности геометрическая изотропия также гарантирует вдоль любой границы или ребра элемента полноту полиномиального представления того же порядка, что и внутри элемента.
Когда в качестве пробной функции выбран полный полином, то элемент обладает геометрической изотропией. Если из полинома исключаются некоторые члены, то это следует сделать так, чтобы элемент, соответствующий неполному полиному, оставался по-прежнему геометрически изотропным. При
определении того, какие члены можно отбросить, ясно, что симметричные пары (как x2, y2 или x3, y3, илиx5y2, x2y5) не вносит несимметричность по отношению к той или иной координате при условии, что порядок исходного полинома не уменьшился.
Для иллюстрации отбрасывания симметричных пар полного полинома, рассмотрим содержащий десять членов полной кубической полином от двух переменных:
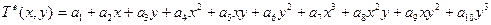 .
.
Элемент, которому соответствует этот полный полином, обладает геометрической изотропией, но то же имеет место при использовании следующих неполных кубических полиномов:
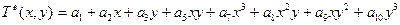 ,
,
или 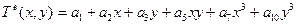 .
.
В последних выражениях кубические члены сохранены, чтобы порядок исходного кубического полинома не уменьшился.
В заключение заметим, что в практике метода конечных элементов полные полиномы, как правило, не употребляются.
 2015-08-21
2015-08-21 618
618








