2015-08-21
585
Задание граничных условий позволяет программно превратить
глобальные матрицы в числовые. В стационарном случае это означает, что
получена система R (по количеству узлов) алгебраических уравнений с числовыми коэффициентами при неизвестных узловых значениях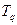 
или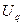 
, которая может быть разрешена с помощью стандартной программы (например, “GELG”, реализующей метод Гаусса).
В нестационарном случае получается система R обыкновенных дифференциальных уравнений первого порядка с числовыми глобальными матрицами [1]:
, 
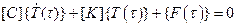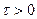, (6.2.1)
с начальным условием, включенным в таблицу данных:
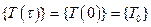. (6.2.2)
Система уравнений (6.2.1) вместе с (6.2.2) представляет собой известную
Таблица 5
Временная циклограмма q(τ)
| Время (мин.) | Номер элемента | Номер поверхности | Величина мощности (Вт) |
| 0 ÷ 30 | |||
| 30 ÷ 60 |
задачу Коши. Для ее решения применим метод конечных элементов, для чего представим (см. рис. 6.1) временную ось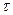 
совокупностью 
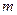отрезков (элементов), не обязательно одинаковой длины 
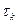, хотя последнее и удобнее. Кривая 
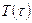дает графическое изображение временной зависимости температуры не в отдельном глобальном r-ом узле, а всего вектора значений температуры в R глобальных узлах, т.е. 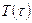– это вектор-столбец размером 
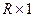. Для отображения этого факта на рисунке применен жирный шрифт.
Используя версию МКЭ, аппроксимирующую функцию на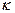 
- м временнόм элементе представим в виде:
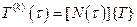, (6.2.3)
где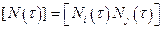 
– матричная строка базисных временных функций;
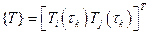– вектор-столбец всей совокупности 
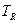значений температу-
ры в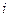 
- м и в 
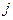- м узлах 
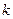- го временнόго элемента.
В качестве базисных функций возьмем линейную модель, которая в естественной системе временных координат имеет вид:
, 
, 
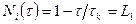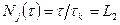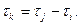(6.2.4)
Применив метод Галеркина к дифференциальному уравнению (6.2.1), для 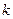- го временнόго элемента получим систему уравнений в интегральной форме:
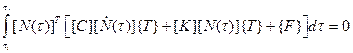. (6.2.5)
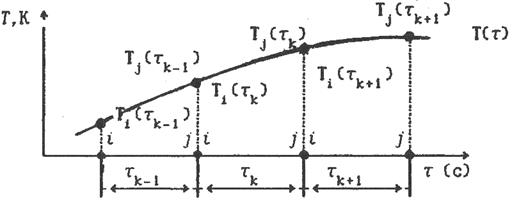
Рис. 6.1
Интегрирование этого выражения с помощью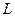 
-координат приводит к системе алгебраических линейных уравнений:
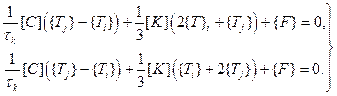
Разрешим ее относительно {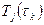 
}:
.
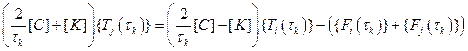Вводя обозначения:
, 
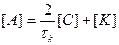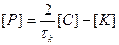, (6.2.6)
последнее выражение запишем компактно:
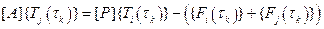. (6.2.7)
Уравнение (6.2.6) содержит две неизвестные – совокупности значений температур 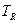в 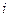- м и в 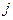- м узлах 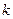- го элемента. Для обеспечения непрерывности интерполяционной функции (6.2.3) в общем для соседних элементов узле должно выполняться условие:
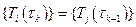. (6.2.8)
Подставляя (6.2.8) в (6.2.7) и опуская одинаковый для всех членов уравнения индекс 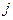, получим рекуррентное уравнение, позволяющее выразить координатные узловые значения температуры на 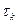- м временнόм шаге через совокупность их значений на предыдущем – 
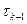- м шаге:
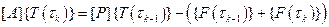. (6.2.9)
Полученное уравнение (6.2.9) может быть решено относительно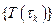 
очевидно только в том случае, если 
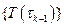известны. Именно это обусловливает обязательную последовательность данного процесса, – он должен начинаться с 
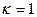с последующим перебором значений 
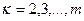. Эта процедура может быть охарактеризована как псевдоитерационный процесс, в котором последующее значение вычисляется по найденному на предыдущем шаге. Отличие заключается в том, что значения в j - м узле находятся по значениям в i - м узле, а в итерационной процедуре значения искомой величины уточняются в одном и том же узле по найденному на предыдущем шаге в этом же узле.
На первом временнόм шаге в качестве 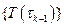будет фигурировать, очевидно, начальное – задаваемое – условие (6.2.2) в 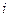- м временном узле, что и позволяет найти по уравнению (6.2.9) значения температур в 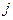- м узле этого же – с 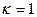– временного элемента:
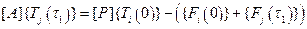. (6.2.10)
Определение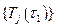 
по уравнению (6.2.10) и, тем самым, согласно (6.2.8) и значений 
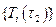в 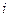- м узле второго временнόго элемента с 
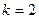, позволяет организовать последовательный процесс в соответствии с рекуррентным уравнением (6.2.9).
Таким образом, методом Галеркина система R дифференциальных уравнений решена и сведена к системе R алгебраических уравнений с числовыми коэффициентами при неизвестных значениях температуры в R глобальных координатных узлах на каждом 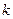- м временнόм элементе.
Другие способы решения системы динамических уравнений (6.2.1) описаны в [2, 6] (решение методом конечных разностей).
