Загальні положення

Моделювання випадкових векторів. Нехай багатовимірна випадкова величина (випадковий вектор) з складовими 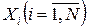задається математичним сподіванням m_i = M [ X_i ] і матрицею кореляційних моментів K_ij (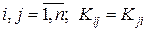) (див. п. 2.6). Складові випадкового вектора Х_і визна­ча­ють­ся як лінійне перетворення некорельованих розподілених за нормальним законом нормованих випадкових величин { V₁, V₂, …, V_m } Î N (0, 1), m = 0, s = 1 за формулами (2.28).

Моделювання випадкових функцій. Алгоритм моделювання реалізації нестаціонарного випадкового процесу, що задається математичним сподіван­ням m_x (t)і кореляційною функцією K_x (t_i, t_j) згідно з п. 2.2,є таким:

· за вхідними даними процесу для всіх дискретних значень функцій у моменти часу 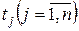визначають дисперсії D (2.31) і координати функції канонічного розкладу f_i (t_i) за виразом (2.29);

· із сукупності випадкових чисел вибирають п чисел і перетворюють їх будь-яким відомим способом у випадкові величини W із заданим розподілом (m_W = 0, D_W = D);

· значення випадкового процесу визначають за формулами (2.32).

У випадку стаціонарних випадкових процесів кореляційна функція K_x (t_i, t_j) = K (t) не залежить від вибору аргументів, а визначається лише їх різницею t = t_j – t_i.

Завдання для виконання роботи

Відповідно до заданого варіанту необхідно виконати наступні дії:

· отримати послідовність реалізацій випадкового вектора;

· побудувати графік зміни реалізації випадкової функції та координатних функцій канонічного розкладу на заданому інтервалі часу;

· визначити кількість реалізацій розподілів випадкового вектора;

· розробити програмний код для реалізації методів моделювання.

Індивідуальні завдання для моделювання

Варіант 1. Стан блоку характеризується тривимірним вектором параметрів 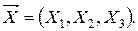Відхилення параметрів від номінальних значень описується нормаль­ним розподілом з нульовим вектором середніх значень 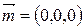та кореля­ційною матрицею

.

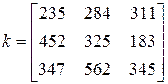Змоделювати стан вектора параметрів для N = 10 блоків.

Варіант 2. Змоделювати N = 15 реалізацій нормального випадкового вектора 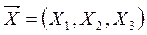з математичним сподіванням 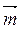= (5,-2,0) та кореляційною матрицею

.

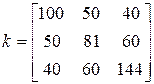Варіант 3. Змоделювати N = 18 реалізацій систем двох випадкових величин (Х₁,Х₂), що підпорядковуються двомірному нормальному закону розподілу з параметрами т₁ = 3, т₂ = 3.5, σ₁ = 4, σ₂ = 5, k ₁₂ = k ₂₁ = 7.

Варіант 4. Випадкова точка (х, у) розподілена за нормальним законом на площині з параметрами т_х = 7, т_у = 18, σ_х = 2, σ_у = 3, k_ху = 0. Змоделювати N = 18 реалізацій випадкової точки.

Варіант 5. Процес зміни напруги на клемах генератора є нестаціонарним випадковим процесом, що задається математичним сподіванням
m(t) = 20 – е ^{–0.2 t} та кореляційною матрицею

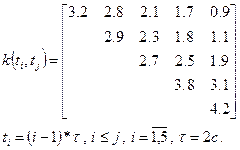
Отримати канонічний розклад випадкового процесу і змоделювати реалізацію напруги на часовому інтервалі [0, 8]с з кроком дискретності відліків τ = 2с.

Варіант 6. Відхилення руху об’єкта від заданої траєкторії є випадковим процесом з нульовим математичним сподіванням і кореляційною функцією 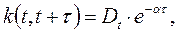де D_t = 5 t + 350, α = 0,08. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію параметра руху на інтервалі [0; 40]с з кроком дискретності відліків τ = 5с.

Варіант 7. Випадкова точка (X,Y)розподілена рівномірно в прямокутнику, який обмежений прямими: х ₁= 0; х ₂ = 3; у ₁= 4; у ₂= 9. Щільність функції розподілу f (x,y)= 0,3 в середині прямокутника та f (x,y) = 0 зовні його. Змоделювати вибірку N = 10реалізацій випадкової точки.

Варіант 8. Випадкова точка (X,Y)розподілена рівномірно в прямокутнику, який обмежений прямими: х ₁= 2; х ₂ = 8; у ₁= 1; у ₂ = 10. Щільність функції розподілу f (x,y)= 0,2 в середині прямокутника та f (x,y) = 0 зовні його. Змоделювати вибірку N = 15реалізацій випадкової точки.

Варіант 9. Змоделювати N = 10 реалізацій тривимірного випадкового вектора з математичним сподіванням 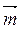= (–5, 10, 25)та кореляційною матрицею

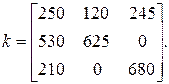
Варіант 10. Відомі характеристики випадкового процесу: m_x (t) = 3 t² + 2 t + 1; 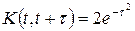. Отримати канонічний розклад випадкового процесу і змоде­лю­вати його реалізацію на інтервалі [0; 50] з кроком дискретності відліків t = 3c.

Варіант 11. Проводиться стрільба по точковій цілі на площині. Розсіяння точки розриву снаряду проходить за нормальним законом, центр якого співпадає з ціллю (т_х = т_у = 0), а кореляційна матриця має вигляд:

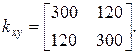
Попадання в ціль відбувається, якщо відстань від неї до точки розриву снаряда не перевищує r₀ = 10м. Змоделювати результати N = 10 пострілів і визначити кількість попадань.

Варіант 12. Похибка автоматичної системи спостереження описується нестаціонарною випадковою функцією з математичним сподіванням m (t) = 0.01 t і кореляційною функцією k (t, t+τ) = 1.2 e^-ατ cos βτ, де α = 0,05; β = 0,04. Отримати канонічний розклад випадкової функції і змоделювати реалізацію похибки на інтервалі [0, 100]с, з кроком дискретності τ =10с.

Варіант 13. Випадковий вектор 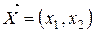розподілений з постійною щіль­ністю f (x,y)в середині квадрату R з вершинами (0, 0); (3,0); (3,3); (0,3), а

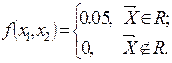
Обґрунтувати метод моделювання і отримати N= 30реалізацій випадкового вектора.

Варіант 14. Частота обертання валу електродвигуна змінюється під впливом випадкових коливань напруги живлення і навантаження на валу та описується нестаціонарною випадковою функцією з математичним сподіванням m (t) = 3∙10³ sin 0.2 t і кореляційною функцією k (t, t + τ) = D_t ∙ е^-ατ, де D_t = 20.5 t; α = 0,05. Отримати канонічний розклад випадкової функції і змоделювати реалізацію частоти обертання валу електродвигуна на інтервалі [0; 40]с, з кроком дискретності τ = 4с.

Варіант 15. Динамічна похибка систем автоматичної зміни частоти описується нестаціонарним випадковим процесом з нульовим математичним сподіван­ням і кореляційною функцією k (t, t + τ) = D_t ∙ е^-ατ cos βτ; D_t = 200 + 5 t; α = 0.2; β = 0.5. Отримати канонічний розклад випадкового процесу і змоделювати реалізацію динамічної похибки системи на інтервалі [0; 20]с з кроком дискретності τ = 2 с.