2015-08-21
332
Звернемося до подання розглянутого руху на фазовій площині. Відома процедура методу ізоклин призводить до їх рівнянь
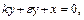(2.6)
де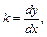 
, 
.
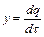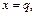
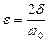Перепишемо рівняння ізоклин (2.6) у вигляді
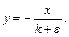(2.7)
Нульова ізоклина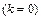 
тепер не збігається з віссю 
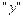і проходить через другий і четвертий квандранти (рис. 2.5), коли 
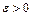(дисипація позитивна). Фазові траєкторії представляють спіралі, що накручуються на початок координат. Особлива точка називається стійким фокусом.
У випадку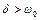 
(режим апериодичного руху) фазовий портрет представляється деформованими параболами (рис. 2.6), а особлива точка називається стійким вузлом.
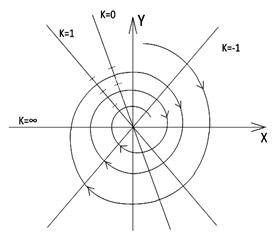
Рисунок 2.5 – Фазовий портрет лінійної системи
зі слабкою дисипацією
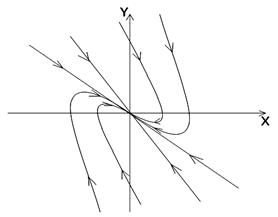
Рисунок 2.6 – Фазовий портрет лінійної системи
з сильним загасанням
