Енергія пружних хвиль

Виділимо в пружному середовищі з щільністю 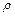, де поширюється плоска хвиля виду 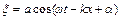, елементарний об'єм 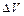. Завдяки хвилі обсяг 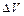набуває швидкість .

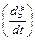Величина кінетичної енергії речовини в об’ємі 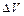дорівнює

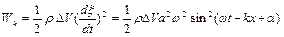. (8.12)

Потенційна енергія деформації об'єму 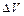дорівнює:

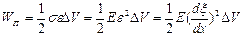. (8.13)
Враховуючи (8.12) та зв'язок 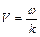, матимемо величину модуля Юнга

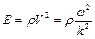(8.14)

Підставляючи (8.14) в (8.13), отримаємо вираз потенційної енергії:

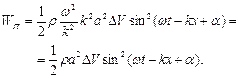(8.15)

Повна енергія об'єму середовища, що приймає участь в хвильовому процесі, дорівнює

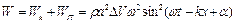. (8.16)

Розділивши (8.16) на 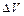, одержимо об'ємну щільність енергії пружної хвилі:

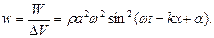
Знайдемо середнє за часом значення об'ємної щільності енергії хвилі. Враховуючи що

,

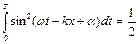одержимо:

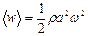. (8.17)

Таким чином, енергія пружної хвилі пропорційна квадрату амплітуди хвилі.