Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
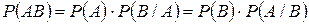 .
.
6. Формула полной вероятности. Формула Байеса
Пусть события (гипотезы) Н1, Н2, …, Нn образуют полную группу событий и при наступлении каждого из них, например Нi, событие A может наступить с некоторой условной вероятностью 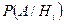 . Тогда вероятность наступления события A равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:
. Тогда вероятность наступления события A равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:
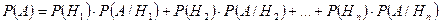
где 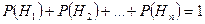 .
.
Данная формула называется формулой полной вероятности.
Пусть событие A может наступить лишь при условии появления одного из несовместных событий (гипотез) Н1, Н2, …, Нn, которые образуют полную группу событий. Если событие A уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса (формуле вероятности гипотез):
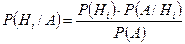 , (
, (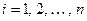 )
)
где 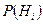 - вероятность каждой из гипотез после испытания, в результате которого наступило событие A;
- вероятность каждой из гипотез после испытания, в результате которого наступило событие A; 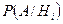 - условная вероятность события A после наступления события Нi, а
- условная вероятность события A после наступления события Нi, а 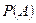 находится по формуле полной вероятности.
находится по формуле полной вероятности.
7. Повторение испытаний. Формула Бернулли
Если производятся испытания, при которых вероятность появления события A в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события A.
Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события A равна p (где 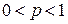 ), событие A наступит ровно k раз (безразлично, в какой последовательности), находится по формуле Бернулли:
), событие A наступит ровно k раз (безразлично, в какой последовательности), находится по формуле Бернулли:
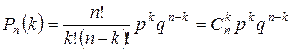 , где
, где 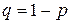 .
.
8. Случайные величины и законы их распределения
Если каждому элементарному событию A из некоторого множества событий ω можно поставить в соответствие определенную величину 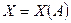 , то говорят, что задана случайная величина. Случайную величину X можно рассматривать как функцию события A с областью определения ω.
, то говорят, что задана случайная величина. Случайную величину X можно рассматривать как функцию события A с областью определения ω.
Если значения, которые может принимать данная случайная величина X, образуют дискретный (конечный или бесконечный) ряд чисел x1, x2, …, xn,…, то и сама случайная величина X называется дискретной.
Если же значения, которые может принимать данная случайная величина X, заполняют целый конечный или бесконечный промежуток 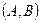 числовой оси Ox, то случайная величина называется непрерывной.
числовой оси Ox, то случайная величина называется непрерывной.
Каждому значению случайной величины дискретного типа xn отвечает определенная вероятность pn; каждому промежутку 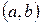 из области значений случайной величины непрерывного типа также отвечает определенная вероятность
из области значений случайной величины непрерывного типа также отвечает определенная вероятность 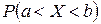 того, что значение, принятое случайной величиной, попадает в этот промежуток.
того, что значение, принятое случайной величиной, попадает в этот промежуток.
Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.
Закон распределения дискретной случайной величины обычно задается рядом распределения:
| xi | x1 | x2 | x3 | … | xn |
| pi | p1 | p2 | p3 | … | pn |
при этом 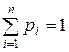 , где суммирование распространяется на все множество возможных значений данной случайной величины X.
, где суммирование распространяется на все множество возможных значений данной случайной величины X.
Закон распределения непрерывной случайной величины удобно задавать при помощи функции плотности вероятности f(x). Вероятность 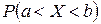 того, что значение, принятое в промежуток
того, что значение, принятое в промежуток 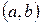 , определяется равенством
, определяется равенством 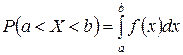 .
.
Функция плотности вероятности обладает следующими свойствами:
1) 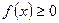 , 2)
, 2) 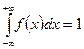 .
.
9. Биномиальный закон распределения. Закон Пуассона
Если вероятность наступления случайного события в каждом испытании равна p, то вероятность того, что при n испытаниях событие A наступит k раз, находится по формуле Бернулли:
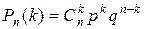 , где
, где 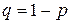 .
.
Закон распределения случайной величины X, которая может принимать n+1 значение (0, 1, …, n), описываемый формулой Бернулли, называется биномиальным.
Закон распределения случайной величины X, которая может принимать любые целые неотрицательные значения (0, 1, …, n), описываемый формулой
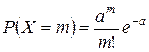 , где
, где 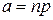
носит название закона Пуассона, дающего более точное значение при малых p.
10. Математическим ожиданием дискретной случайной величины называется сумма произведений значений случайной величины на вероятности этих значений:
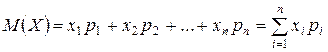
Математическое ожидание непрерывной случайной величины X определяется равенством
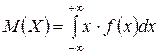 (при условии, что значение этого интеграла конечно).
(при условии, что значение этого интеграла конечно).
11. Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
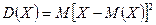 .
.
Легко получить для вычисления дисперсии более удобную формулу:
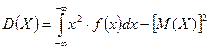
Дисперсия случайной величины есть мера рассеяния ее значений около ее математического ожидания.
Средним квадратическим отклонением случайной величины X называется величина 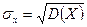 .
.
12. Свойства математического ожидания случайной величины:
1. 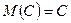 , где
, где 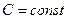 ;
;
2. 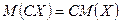 , где
, где 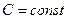 ;
;
3. 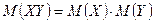 , где X и Y – независимые случайные величины;
, где X и Y – независимые случайные величины;
4. 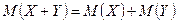 .
.
13. Свойства дисперсии случайной величины:
1. 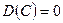 , где
, где 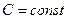 ;
;
2. 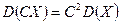 , где
, где 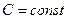 ;
;
3. 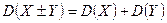 , где X и Y – независимые случайные величины.
, где X и Y – независимые случайные величины.
Пример 1. Среди 30 курсантов взвода 8 отличников. Для внеочередного дежурства назначено 5 курсантов. Найти вероятность того, что среди дежурных отличников будет нечетное число.
Решение. Введем обозначения: 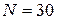 ,
, 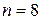 ,
, 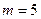 ,
, 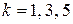 . Общее число возможных элементарных исходов испытания равно числу способов, которыми можно назначить m курсантов из N курсантов, т.е.
. Общее число возможных элементарных исходов испытания равно числу способов, которыми можно назначить m курсантов из N курсантов, т.е. 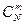 – числу сочетания из N элементов по m.
– числу сочетания из N элементов по m.
Посчитаем число исходов, благоприятствующих интересующему нас событию (среди m курсантов ровно k отличников): k отличников можно выбрать из n отличников 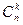 способами, при этом остальные
способами, при этом остальные 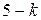 курсантов выбираются из
курсантов выбираются из 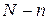 курсантов
курсантов 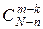 способами,
способами, 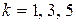 . Следовательно, число благоприятствующих исходов равно
. Следовательно, число благоприятствующих исходов равно 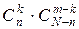 . События, состоящие в том, что число отличников среди выбранных пяти курсантов 1, 3 или 5, являются несовместными. По теореме сложения вероятностей для несовместных событий получаем:
. События, состоящие в том, что число отличников среди выбранных пяти курсантов 1, 3 или 5, являются несовместными. По теореме сложения вероятностей для несовместных событий получаем:
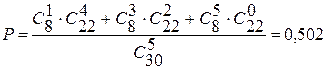 ,
,
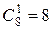 ,
, 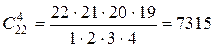 ,
, 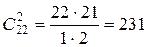 ,
,
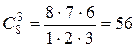 ,
, 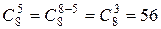 ,
, 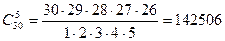 ,
, 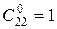 .
.
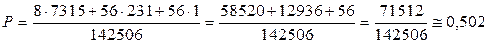 .
.
Пример 2. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго - 0,8. Найти вероятность того, что:
a) попадет только первый стрелок;
b) попадет только один стрелок;
c) попадут оба стрелка;
d) не попадет никто;
e) попадет хотя бы один стрелок.
 2015-08-21
2015-08-21 4774
4774
