Решение

Введем обозначения:

A₁ = {первый стрелок попал в мишень};

A₂ = {второй стрелок попал в мишень}.

Тогда

P(A₁) = 0,7; P(A₂) = 0,8; 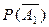= 1 - 0,7 = 0,3; 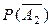= 1 - 0,8 = 0,2

А = {попадет только первый стрелок}.

Выразим событие А через события A₁ и :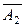

А = A₁ × .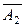

Т. к. события A₁ и 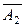- независимы, то применим теорему умножения для независимых событий.

P(A₁ × 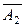) = P(A₁)×P(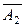) = 0,7 × 0,2 = 0,14

B = {попадет только один стрелок}.

В = A₁ × 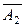+ A₂ × .

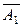Т.к. события A₁ × 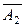и A₂ × 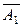- несовместны и независимы, то применим соответствующие теоремы сложения и умножения

P(A₁ × 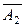+ A₂ × 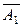) = P(A₁)×P(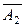)+ P(A₂)×P(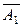) = 0,7 × 0,2 + 0,8 × 0,3 =

= 0,14 + 0,24 = 0,38.

C = {попадут оба стрелка}.

С = A₁ ×A₂.

Т.к. события A₁ и A₂ - независимы, то применим теорему умножения:

P(A₁ ×A₂) = P(A₁)×P(A₂) = 0,7×0,8 = 0,56.

D = {не попадет ни один стрелок}.

D = × .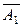

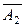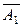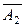Т.к. события и - независимы, то применим теорему умножения:

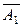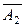P( 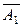× ) = P()×P(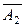) = 0,3 × 0,2 = 0,06.

E = {попадет хотя бы один стрелок}.

Применим теорему о появлении хотя бы одного из независимых событий:

P(E) = 1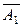 - P()×P(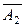) = 1 - 0,06 = 0,94.

Пример 3. Из 20 пассажиров автобуса 5 едут в г. Иваново. Какова вероятность того, что из двух наугад выбранных пассажиров

только один едет в г. Иваново;

оба едут в г. Иваново;

хотя бы один едет в г. Иваново.