Что такое система одновременных эконометрических уравнений? Чем она отличается от набора регрессионных уравнений?

Ответ:

СОУ – набор уравнений регрессии и тождеств, в которых одни и те же переменные могут играть роль объясняющих и объясняемых переменных.

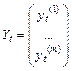- зависимые – эндогенные переменные, 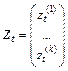- объясняющие – экзогенные, 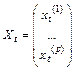- предопределенные переменные (экзогенные + лагированные эндогенные (переменные в предыдущий момент времени)).

Общая запись СОУ: 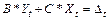- СОУ – структурная форма. – система из m ур-ний.

(m*m) (m*p) (m*1)

Решаем i-ое уравнение этой системы: 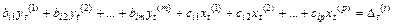, i=1,2,…,n, располагая наблюдениями (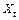, 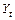), t=1,2,…, n - исходные данные. Нужно найти оценки коэффициентов модели, т.е. 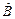и 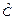. Для этого используем дополнительное условие невырожденности матрицы В, т.е. домножим правую и левую часть на матрицу 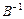. Т.о. получаем 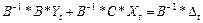, перенеся у в левую часть, а все остальное в правую получается приведенная форма - 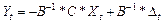, или еще можно записать так: 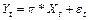. Получаем систему уравнений. Эта система будет идентифицирована, если все уравнения идентифицированы, а уравнения будут идентифицированы, если все их коэффициенты будут идентифицированы, т.е. выражены в терминах матрицы 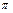(условия идентифицированности:. И для оценки коэффициентов матрицы находим оценку матрицы 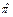методом наименьших квадратов, если остатки не коррелируют друг с другом.

Специфика системы состоит в том, что в каждом уравнении может присутствовать эндогенные переменные, как объясняющие переменные, а так же эндогенные переменные могут выступать в роли как результирующих, так и объясняемых переменных в одном и том же уравнении.