Вал, вращающийся со скоростью w, выведен из состояния равновесия возмущающей силой (импульсом силы).
При этом возникнут следующие деформации этого вала:
- 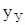 – упругий прогиб вала;
– упругий прогиб вала;
- 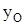 – деформация опор.
– деформация опор.
Кроме этого, следует учесть и наличие эксцентриситета вала ye. В результате центр тяжести массы m будет вращаться на расстоянии 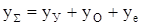 от первоначального (идеального) положения оси вала 0-0 (рис. 23).
от первоначального (идеального) положения оси вала 0-0 (рис. 23).
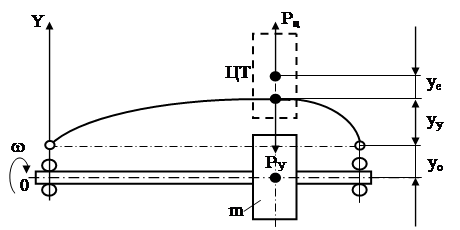
Рис. 23. Вал с одной массой
На вал будут действовать две противонаправленные силы – центробежная сила и сила упругости.
Центробежная сила равна

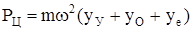 , (194)
, (194)
а сила упругости изогнутого вала
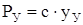 . (195)
. (195)
В результате можно выделить три возможных ситуации:
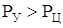 – вал вернется в положение равновесия;
– вал вернется в положение равновесия;
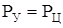 – критическое состояние;
– критическое состояние;
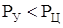 – неуправляемый рост деформации вала до разрушения.
– неуправляемый рост деформации вала до разрушения.
Рассмотрим ситуацию 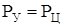 , которой соответствует критическая скорость вращения
, которой соответствует критическая скорость вращения 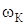 .
.
В результате преобразований из равенства уравнений (194) и (195) получим
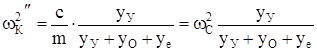 , (196)
, (196)
где 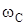 – собственная частота колебаний системы.
– собственная частота колебаний системы.
Если не учитывать эксцентриситет (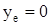 ) и деформацию опор (
) и деформацию опор (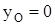 ), то из (196) найдем
), то из (196) найдем
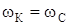 . (197)
. (197)
Это явление называется резонансом системы.
В свою очередь 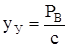 и
и 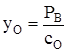 ,
,
где 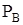 – возмущающая сила,
– возмущающая сила,
c – жесткость вала,
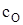 – жесткость опор.
– жесткость опор.
Тогда
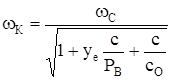 . (198)
. (198)
Рассмотрим частный случай, когда не учитывается деформация опор (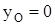 ). Тогда из формулы (196) получим
). Тогда из формулы (196) получим
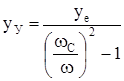 . (199)
. (199)
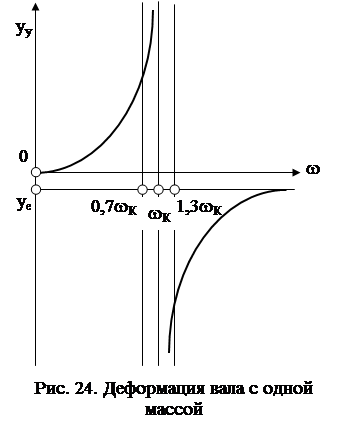
Характер деформации вала в зависимости от скорости его вращения показан на рис. 24. Видно, что согласно формуле (199), прогиб вала yУ по мере приближения w к wК растет и при 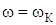 становится равным
становится равным 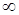 . В закритической области
. В закритической области 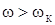 наблюдается самоустановка вала с
наблюдается самоустановка вала с 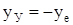 .
.
Для перехода через критическую область 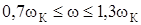 применяют демпфирующие устройства, позволяющие уменьшить wС за счет снижения жесткости системы c.
применяют демпфирующие устройства, позволяющие уменьшить wС за счет снижения жесткости системы c.
 2015-08-21
2015-08-21 304
304








