Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 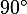 . Другими словами, половина развернутого угла.
. Другими словами, половина развернутого угла.
Острый угол — меньший 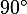 .
.
Тупой угол — больший 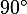 . Применительно к такому углу «тупой» — не оскорбление, а математический термин:-)
. Применительно к такому углу «тупой» — не оскорбление, а математический термин:-)

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается 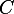 . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла
. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла 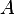 , обозначается
, обозначается 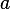 .
.
Угол 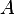 обозначается соответствующей греческой буквой
обозначается соответствующей греческой буквой 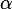 .
.
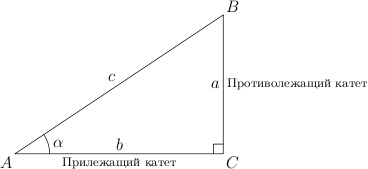
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет 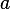 , лежащий напротив угла
, лежащий напротив угла 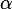 , называется противолежащим (по отношению к углу
, называется противолежащим (по отношению к углу 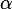 ). Другой катет
). Другой катет 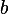 , который лежит на одной из сторон угла
, который лежит на одной из сторон угла 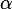 , называется прилежащим.
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
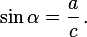
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
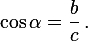
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
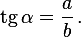
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
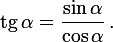
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
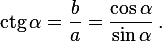
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
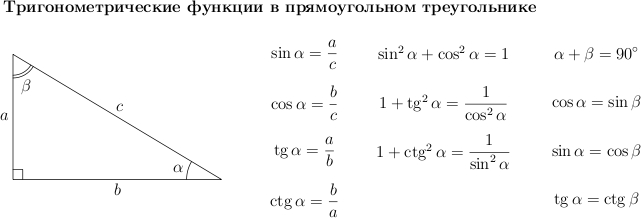
Давайте докажем некоторые из них.
1. Сумма углов любого треугольника равна 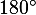 . Значит, сумма двух острых углов прямоугольного треугольника равнa
. Значит, сумма двух острых углов прямоугольного треугольника равнa 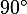 .
.
2. С одной стороны, 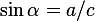 как отношение противолежащего катета к гипотенузе. С другой стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны, 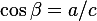 , поскольку для угла
, поскольку для угла 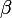 катет
катет 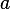 будет прилежащим.
будет прилежащим.
Получаем, что 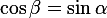 . Иными словами,
. Иными словами, 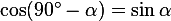 .
.
3. Возьмем теорему Пифагора: 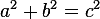 . Поделим обе части на
. Поделим обе части на 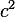 :
:
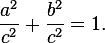
Мы получили основное тригонометрическое тождество:
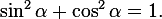
Таким образом, зная синус угла, мы можем найти его косинус, и наоборот.
4. Поделив обе части основного тригонометрического тождества на 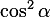 , получим:
, получим:
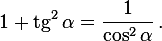
Это значит, что если нам дан тангенс острого угла 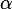 , то мы сразу можем найти его косинус.
, то мы сразу можем найти его косинус.
Аналогично,
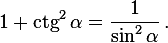
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна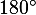 .
.
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: 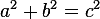 .
.
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
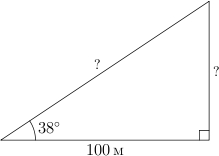
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от 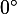 до
до 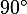 .
.
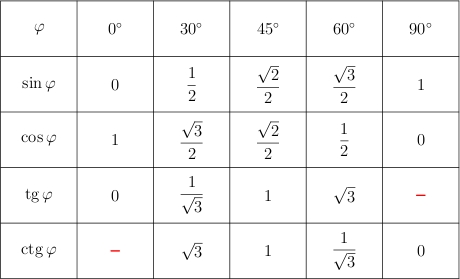
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике 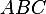 угол
угол 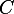 равен
равен 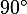 ,
, 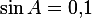 . Найдите
. Найдите 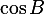 .
.
Задача решается за четыре секунды.
Поскольку 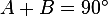 , имеем:
, имеем: 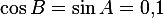 .
.
2. В треугольнике 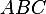 угол
угол 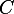 равен
равен 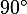 ,
, 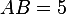 ,
, 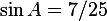 . Найдите
. Найдите 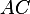 .
.
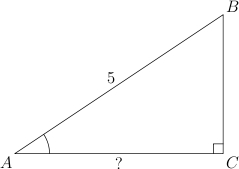
Имеем:
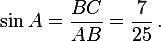
Отсюда
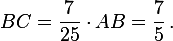
Теперь находим 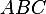 по теореме Пифагора:
по теореме Пифагора:
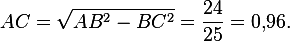
Задача решена.
Часто в задачах встречаются треугольники с углами 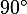 ,
, 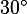 и
и 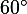 или с углами
или с углами 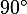 ,
, 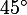 и
и 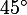 . Основные соотношения для них запоминайте наизусть!
. Основные соотношения для них запоминайте наизусть!
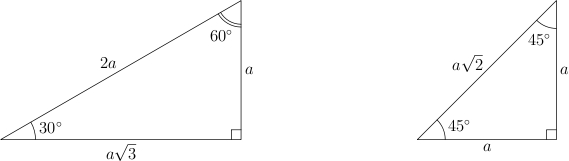
Для треугольника с углами 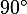 ,
, 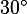 и
и 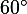 катет, лежащий напротив угла в
катет, лежащий напротив угла в 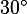 , равен половине гипотенузы.
, равен половине гипотенузы.
Треугольник с углами 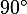 ,
, 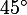 и
и 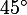 — равнобедренный. В нем гипотенуза в
— равнобедренный. В нем гипотенуза в 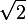 раз больше катета.
раз больше катета.
 2015-09-07
2015-09-07 12214
12214








