Доказательство в геометрии

Важнейшей научной заслугой Пифагора считается систематическое введение доказательства в математику, и прежде всего в геометрию.

Строго говоря, только с этого момента математика и начинает существовать как наука, а не как собрание древнеегипетских и древневавилонских практических рецептов. С рождением же математики зарождается и наука вообще, ибо «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» (Леонардо да Винчи).

Что же такое математическое доказательство? Допустим, на ряде примеров мы обнаружили некую математическую закономерность. Значит ли это, что она справедлива всегда? Отнюдь. Таких примеров в математике предостаточно. Скажем, известные нам числа Ферма 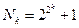. Они являются простыми при 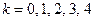. Одно время казалось, что все числа Ферма являются простыми, пока Эйлер не обнаружил у числа 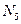делитель. Но следует ли отсюда, что все числа Ферма при 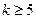являются составными? Тоже нет. Из того, что мы не знаем простых чисел Ферма при 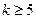, еще не следует, что их не существует вообще. Вопрос о свойствах чисел Ферма при 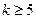просто не решен, не доказан. Но ясно, что доказывать его нужно для любого k, т. е. для бесконечного множества значений k, ибо в противном случае у нас не будет уверенности в том, что следующее значение не даст числа с противоположными свойствами.

Другой пример. Пусть мы хотим установить, чему равна сумма углов треугольника. Измерив десяток-другой треугольников, мы легко обнаружим, что эта сумма колеблется где-то около 180°, хотя вряд ли мы хоть раз получим точно 180° или два одинаковых результата. Эти разночтения вызваны как погрешностью наших измерений, так и погрешностью самих измеряемых объектов, которые не являются идеально прямолинейными фигурами. Делая скидку на эти ошибки, мы можем предположить, что сумма углов треугольника все-таки равна 180°, хотя никакой уверенности в этом у нас быть не может, ибо треугольников существует опять-таки бесконечное множество.

Так вот, заслуга Пифагора и состояла в том, что он, по-видимому, первым пришел к следующей мысли: в геометрии, во-первых, должны рассматриваться абстрактные идеальные объекты (точки — «то, что не имеет частей», линии — «длина без ширины», поверхности — «то, что имеет только длину и ширину» и т. д.) и, во-вторых, свойства этих идеальных объектов должны устанавливаться не с помощью измерений на конечном числе объектов, а с помощью рассуждений, справедливых для бесконечного числа объектов. Эта цепочка рассуждений, которая с помощью законов логики сводит неочевидные утверждения к известным или очевидным истинам, и есть математическое доказательство.

Но на этом пути математика подстерегает другая опасность. Избежав рассмотрения бесконечного множества объектов, у нас нет никакой уверенности в том, что цепочка рассуждений, приводящая неочевидное утверждение A к очевидной истине, сама не окажется бесконечной:

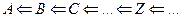
Правда, эту бесконечность можно легко устранить, оборвав на каком-то этапе цепочку рассуждений, и приняв последнее утверждение Ζ за очевидную истину. Однако эта легкость обманчива, ибо здесь возникает новая опасность: в каждой цепочке рассуждений последняя «очевидная» истина, на которой мы оборвем цепочку, может быть своя, и поскольку мы вряд ли захотим ограничить себя конечным числом доказываемых истин, то и число «последних» предложений может оказаться бесконечным.

И вот следующая гениальная догадка Пифагора (или его учеников) состояла в том, что в геометрии можно выбрать именно конечное число первоначальных истин, из которых с помощью логических правил выводимо неограниченное число геометрических предложений. Эти отправные недоказуемые («очевидные») положения были названы аксиомами (’αξίωμα — ценность, основное положение).

Так в геометрии впервые возник аксиоматический метод построения науки. Начало этому методу было положено на рубеже VI — V вв. до н. э. в школе Пифагора, а уже в III в. до н. э. в «Началах» Евклида грандиозная программа аксиоматизации геометрии была полностью завершена. Число первоначальных, принимаемых без доказательства утверждений — аксиом — было сведено к минимуму, а все остальные геометрические истины — теоремы — получались из них цепочкой логических рассуждений — доказательств. Так родилась триада аксиома — доказательство — теорема, которая и составила ядро нового метода.

Выработка системы аксиом — это долгий и кропотливый процесс накопления первоначальных факторов, их проверки, перепроверки, систематизации, уточнения и исключения лишних либо, наоборот, обнаружения недостающих. В этом процессе и рождается система аксиом — минимальная совокупность первоначальных утверждений, необходимая и достаточная для доказательства (или опровержения) любого нового утверждения.

Итак, аксиоматическое построение геометрии или любой другой науки (например, механики) заключается в следующем:

1. Перечисляются первоначальные неопределимые понятия. (Эти изначальные понятия можно лишь описать, но не определить. Так, определение 1 Евклида: «Точка есть то, что не имеет частей» — есть фактически лишь описание неопределимого понятия точки.)

2. Составляется система аксиом, описывающих свойства этих неопределимых понятий и взаимоотношений между ними.

3. С помощью определений вводятся новые понятия, сводимые к неопределимым.

4. С помощью теорем доказываются новые утверждения, вытекающие из системы аксиом.

К системе аксиом предъявляются три важнейших требования: непротиворечивость, полнота и независимость. Непротиворечивость состоит в том, что из данной системы аксиом нельзя получить две теоремы, противоречащие друг другу. Полнота обеспечивает логическое следствие из системы аксиом всех верных утверждений. Наконец, независимость означает, что каждая аксиома не является логическим следствием, т. е. «независима» от остальных аксиом данной системы.

Одновременно с разработкой аксиоматического метода развивались и методы перехода от одних истинных утверждений к другим, т. е. методы построения цепочки рассуждений, именуемой доказательством. Одним из таких приемов был метод приведения к противоречию, которым пифагорейцы доказали несоизмеримость стороны и диагонали квадрата и который в V в. до н. э. становится необычайно популярным.

В это же время южноиталийский философ Парменид (ок. 540 до н. э. —?), идейно связанный с пифагорейцами, формулирует закон исключенного третьего, состоящий в том, что из двух противоположных утверждений одно и только одно является истинным. В следующем, IV в. до н. э. Аристотель проводит формализацию и каталогизацию правил умозаключений и высказывает утверждение об их конечности. Эта догадка Аристотеля не менее поразительна, чем гипотеза пифагорейцев о конечном числе аксиом геометрии. Так вместе с разработкой аксиоматического метода зарождалась и новая наука о приемлемых способах рассуждений — логика (λόγος — слово, суждение).

Но вернемся к задаче о сумме углов треугольника. Предание приписывает первое доказательство этой теоремы Пифагору. К сожалению, доказательство Пифагора не сохранилось, поэтому рассмотрим, как доказывает эту теорему Евклид. Обратим внимание на то, что каждый шаг в евклидовой цепочке доказательств обоснован. Именно так и должно строиться всякое математическое доказательство! Свои теоремы Евклид называет предложениями (предложения мы будем обозначать буквой П, аксиомы — А, определения — О). Мы сохраняем формулировки Евклида, хотя текст доказательств приближаем к современному. Обоснование каждого шага доказательства указано в скобках.

Итак, в книге I «Начал» Евклида мы находим:

П.32. Во всяком треугольнике по продолжении одной из сторон внешний угол равен двум внутренним и противолежащим и внутренние три угла треугольника вместе равны двум прямым.

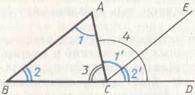
Рис. 52.

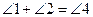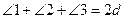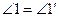Доказательство. Требуется доказать (рис. 52): и . Через точку C проведем прямую . Тогда и 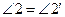(Π.29), откуда 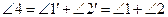(О.8). Итак, 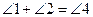. Тогда 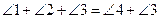(A.2). Но 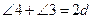(П.13), тогда 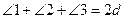(А.1). Что и требовалось доказать.

Как видим, при доказательстве П.32 Евклид использует П.29, П.13, А.2 и О.8.

П.29. Прямая, падающая на параллельные прямые, образует накрест лежащие углы, равные между собой, и внешний угол, равный внутреннему, противолежащему с той же стороны, и внутренние односторонние углы, вместе равные двум прямым.

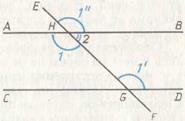
Рис. 53.

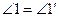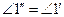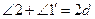Доказательство. Требуется доказать (рис. 53): , и . Доказательство проводим методом от противного. Пусть 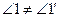. Положим для определенности 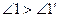, тогда 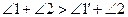(А.2). Но 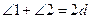(П.13), и, следовательно, 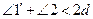. Тогда по 5-му постулату[45] прямые AB и CD пересекаются, а по условию они параллельны. Получили противоречие. (Случай 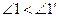доказывается аналогично.) Итак, 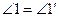. Но 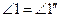(П.15), и, значит, 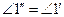(А.1). Тогда 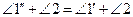(Α.2). Но 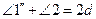(П.13), следовательно, 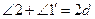. Что и требовалось доказать.

В этом доказательстве использованы П.15, П.13, А.1, А.2 и постулат 5.

П.15. Εсли две прямые пересекаются, то образуют углы через вершину[46], равные между собой.

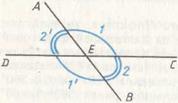
Рис. 54.

Доказательство. Требуется доказать (рис. 54): 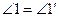и 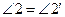; 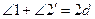(П.13). Аналогично 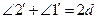(П.13). Тогда 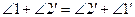(А.1), откуда 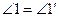(А.3). Аналогично доказывается, что 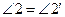. Доказательство завершено.

Здесь использованы П.13, А.1 и А.3.

П.13. Если прямая, восставленная к прямой, образует углы, то она будет образовывать или два прямых, или вместе равные двум прямым.

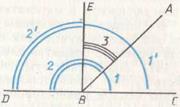
Рис. 55.

Доказательство. Требуется доказать (рис. 55): 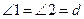или 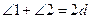. Если 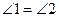, то 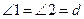(О.10). Если это не так, то восставим в точке B перпендикуляр 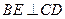. Тогда 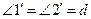(О.10). Но 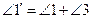(О.8), тогда 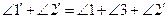(А.2). Но 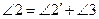(О.8), тогда 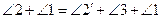(А.2). Следовательно, 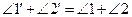(А.1). Но 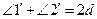(О.10), откуда 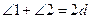(А.1). Что и требовалось доказать.

В последнем доказательстве использованы только аксиомы и определения, т. е. цепочка доказательств здесь обрывается. Нам остается лишь перечислить использованные определения, постулаты и аксиомы.

О.8. Плоский же угол есть наклонение друг к другу двух линий, в плоскости встречающихся друг с другом, но не расположенных по одной прямой.

О.10. Когда же прямая, восставленная к другой прямой, образует рядом углы, равные между собой, то каждый из равных углов есть прямой, а восставленная прямая называется перпендикуляром к той, на которой она восставлена.

Постулат 5. И если прямая, падающая на две прямые, образует внутренние по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встретятся с той стороны, где углы меньшие двух прямых.

А.1. Равные одному и тому же равны и между собой.

А.2. И если к равным прибавляются равные, то и целые будут равны.

А.3. И если от равных отнимаются равные, то остатки будут равны.

Итак, доказательство теоремы о сумме углов треугольника проводится следующей цепочкой утверждений:

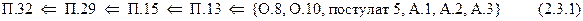
Эту цепочку можно протянуть через все XIII книг Евклидовых «Начал» вплоть до последнего положения последней XIII книги — предложения о существовании только пяти правильных многогранников (см. с. 152)!

Логическая безупречность доказательств Евклида потрясает! Трудно осознать, что столь безукоризненная отточенность математической мысли была достигнута в III в. до н. э.! Вот почему более двух тысячелетий, вплоть до 1899 г., когда выдающийся немецкий математик Давид Гильберт (1862 — 1943) предложил более строгую аксиоматику евклидовой геометрии, «Начала» Евклида оставались недосягаемым образцом логической строгости и завершенности в математике.

Что касается доказательства самого Пифагора, то полагают, что оно было получено как следствие из важнейшей пифагорейской теоремы о покрытии плоскости тремя правильными фигурами (с. 147). Легко заметить, что в точке A (см. рис. 42) сходятся шесть углов равносторонних треугольников. Но 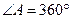, откуда угол в равностороннем треугольнике равен 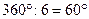, а значит, сумма трех углов составит 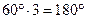. Далее эта теорема была обобщена на случай произвольного треугольника.

Итак, начиная с Пифагора доказательство становится могучим и единственным способом обретения истины в геометрии, а начиная с Евклида аксиоматический метод построения геометрии является образцом отточенности научной мысли. Лишь в XVII в. человечество обрело силы дерзнуть на подобный научный подвиг: в 1687 г. в грандиозном труде «Математические начала натуральной философии» Исааком Ньютоном (1648 — 1727) было дано построение механики на основе аксиоматического метода по образцу «Начал» Евклида.

Вообще, XVII век стал веком расцвета аксиоматического метода. Универсальный гений — философ, математик, физик, юрист, историк, языковед, дипломат и тайный советник Петра I — Готфрид Вильгельм Лейбниц (1646 — 1716) много сил отдал составлению «Алфавита человеческого мышления», из которого можно было бы получить все истинные высказывания, так чтобы «химеры, которые не понимает даже тот, кто их выдвигает, не могли быть записаны в этих знаках». Нидерландский философ Бенедикт Спиноза (1632 — 1677) пытался аксиоматизировать этику, а французский математик и астроном, «Ньютон Франции» Пьер Симон де Лаплас (1749 — 1827) —юридические науки. Увы, эти попытки не дали ожидаемых результатов: слишком сложным и противоречивым оказался предмет исследований.

С 1939 г. группа французских математиков, объединившихся под псевдонимом Никола Бурбаки, пытается осуществить идею Гильберта — изложить всю математику с единых позиций формального аксиоматического метода. В многотомном и далеком от завершения трактате Н. Бурбаки «Элементы математики»[47] развивается формальная аксиоматическая система, которая, по замыслу авторов, должна охватить если не все, то главнейшие разделы математики как частные случаи единой общей концепции.

Так в наши дни продолжают успешно развиваться великие идеи, заложенные на заре цивилизации Пифагором.